Moment of Inertia | Disc

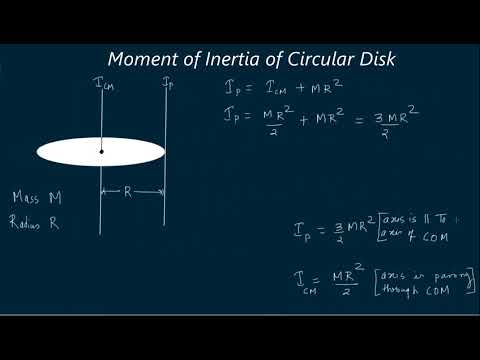
A solid disk with mass M can be conceptualized as a composition of N discrete rings. Each of these rings possesses mass proportionate to the linear density M/(2π⋅Total Length), thereby accommodating rings of distinct masses. The outermost ring exhibits the highest mass. As the quantity of discrete rings augments, the moment of inertia associated with this discretized representation converges toward the moment of inertia value exhibited by a continuous solid disk.

The animation was done by fortran and using gnuplot to its visualization.