filmov
tv
Interpreting Motion Graphically (1 of 4: Direction of movement)

Показать описание
Interpreting Motion Graphically (1 of 4: Direction of movement)
Interpreting Motion Graphs
Position/Velocity/Acceleration Part 2: Graphical Analysis
Velocity Time Graphs, Acceleration & Position Time Graphs - Physics
GCSE Physics - Distance-Time Graphs #53
Interpreting direction of motion from velocity-time graph | AP Calculus AB | Khan Academy
Interpreting Motion Graphically (4 of 4: Velocity & acceleration graphs)
Interpreting direction of motion from position-time graph | AP Calculus AB | Khan Academy
VELOCITY TIME GRAPH (2) | Well Explained | #ganiyuabubakar #excellentlinkacademy #physics
GCSE Physics - Velocity Time Graphs #54
How To Find The Acceleration From a Velocity Time Graph - Physics
How Do You Graph Motion? | Physics in Motion
Velocity time graph
Velocity Time Graphs | Force and Motion | Physics | FuseSchool
Distance (position) to Velocity Time Graph Physics Help
Position-time graphs | One-dimensional motion | AP Physics 1 | Khan Academy
Interpreting Motion Graphically (3 of 4: Exploring acceleration)
Displacement Time graph || Velocity Time graph || Motion in one dimension || Understanding graphs
Interpreting Motion Graph Sketches
Physics 1 | Kinematics | Reading Position Graph
Interpreting Motion Graphically (2 of 4: Identifying specific features)
Physics Motion Graphs
Draw Bar Graph | Easy drawing | #drawings #shorts
Motion Graphs | Velocity-Time Graph and Displacement-Time Graph
Комментарии
 0:11:13
0:11:13
 0:07:31
0:07:31
 0:08:02
0:08:02
 0:31:01
0:31:01
 0:04:01
0:04:01
 0:01:46
0:01:46
 0:08:08
0:08:08
 0:02:39
0:02:39
 0:12:08
0:12:08
 0:05:10
0:05:10
 0:12:44
0:12:44
 0:07:35
0:07:35
 0:08:02
0:08:02
 0:03:25
0:03:25
 0:08:08
0:08:08
 0:05:01
0:05:01
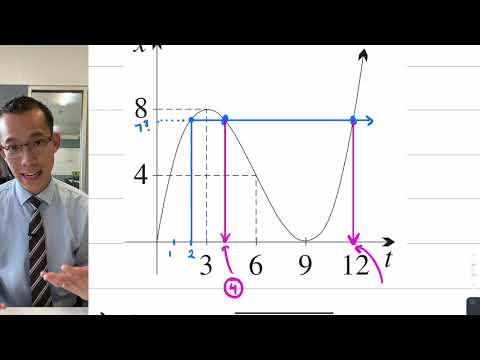 0:10:13
0:10:13
 0:35:00
0:35:00
 0:11:06
0:11:06
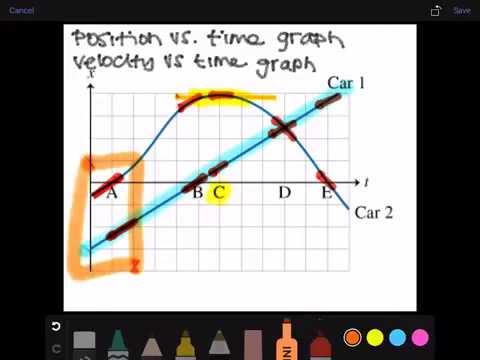 0:02:40
0:02:40
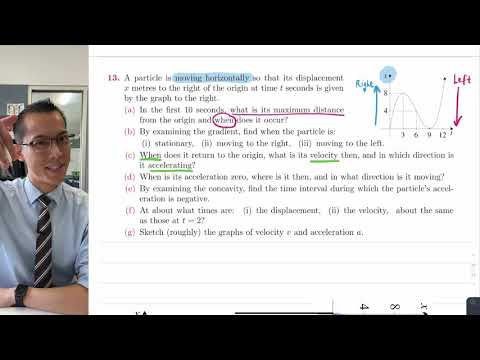 0:08:11
0:08:11
 0:15:01
0:15:01
 0:00:16
0:00:16
 0:01:24
0:01:24