13-60 | Kinetics of a Particle | Chapter 13: Hibbeler Dynamics 14th | Engineers Academy

Do Like this Video if it helps and SUBSCRIBE Engineers Academy for More Problem Solutions!

Chapter 13: Kinetics of a Particle : Force and Acceleration
Equations of Motion: Normal and Tangential Coordinates
Hibbeler Dynamics 14th ed

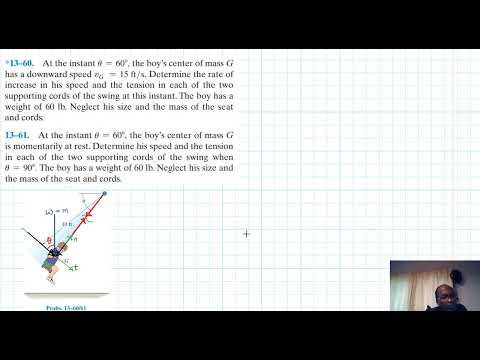
*13–60. At the instant u = 60, the boy’s center of mass G has a downward speed vG = 15 ft/s. Determine the rate of increase in his speed and the tension in each of the two supporting cords of the swing at this instant. The boy has a weight of 60 lb. Neglect his size and the mass of the seat
and cords.

13–61. At the instant u = 60, the boy’s center of mass G is momentarily at rest. Determine his speed and the tension in each of the two supporting cords of the swing when u = 90. The boy has a weight of 60 lb. Neglect his size and the mass of the seat and cords.

#EngineeringMechanics #Dynamics #Hibbeler #Chapter13 Hibbeler Statics - Chapter Playlists

[benjaminjones]

Why do we not assume velocity is only in the tangent direction and find an x component of velocity as well? The way its phrased, by giving Vg Instead of just saying V implies this to me.

[davidleintz]

Hello sir, I am not convinced. The first half makes sense: finding velocity. But when finding tension, wouldn't you need a new free body diagram when theta=90. So, 2T-mg=mv^2/r?

[aaroncarreterob]

I think you had to find he magnitude of acceleration for the first one, which you get from both tangential and normal acceleration values.

[AleEDU-yx]

Velocity used in v^2/r must be perpendicular to normal acceleration so it must be 15cos(60)

[yusufaguib]

Why are you not using the normal force entered by the seat on the boy in your calculations?, so why would it not be 2T + n - 60sin(theta) = 60/32.2 x v^2/10