filmov
tv
SFU MATH 232 7.6 The Pivot Theorem

Показать описание
SFU Math 232 7.6 The Pivot Theorem and Its Implications. This lecture covers the pivot theorem which states that the pivot columns of a matrix form a basis for the matrix's column space. This is then used to take a subspace spanned by k vectors and produce from that a basis for the subspace.
SFU MATH 232 7.6 The Pivot Theorem
SFU MATH 232 7.4 The Dimension Theorem and Its Implications
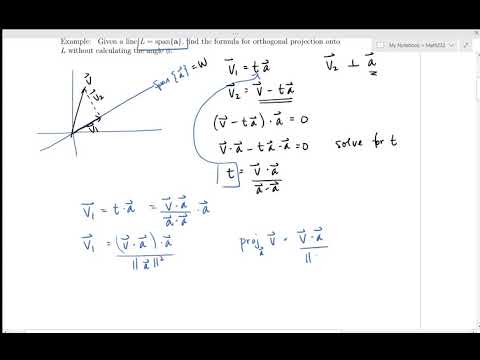
SFU MATH 232 7.7 The Projection Theorem
SFU MATH 232 7.3 Fundamental Spaces of a Matrix
SFU MATH 232 7.5 The Rank Theorem
SFU MATH 232 7.2 Properties of Bases
SFU MATH 232 7.3 Method of Least Squares (Spring 2022) 7.8 Best Approx and Least squares (Fall 2021)
SFU MATH 232 6.3 Applications of Diagonalization
SFU MATH 232 7.2 Projections and the Gram Schmidt Process
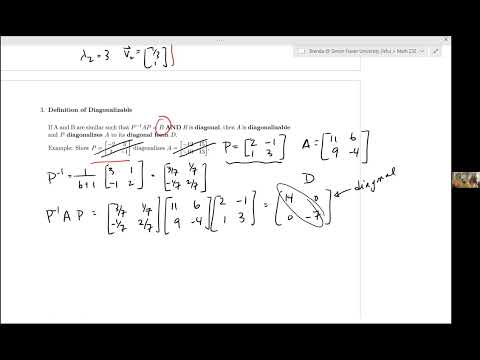
SFU MATH 232 6.2 Diagonalization
SFU MATH 232 Appendix B Complex Numbers
SFU MATH 232 Sec 4 6 worked examples part 1
SFU MATH 232 6.1 Eigenvalues and Eigenvectors - PART 1
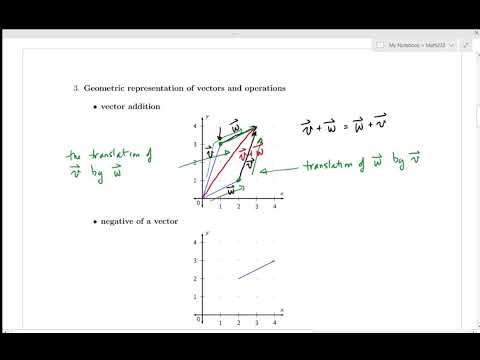
SFU MATH 232 1.1 Vectors and Matrices, n space
SFU MATH 232 4.1 Determinants and Cofactor Expansion
SFU MATH 232 Sec 2.1 Systems of Linear Equations and Elimination
SFU MATH 232 3.1 Operations on Matrices
SFU MATH 232 2.4 Applications to Systems of Linear Equations
SFU MATH 232 Sec 1.5 Dot Products and Projections in R^n
SFU MATH 232 3.5 The Geometry of Linear Systems
SFU MATH 232 4.4 A First Look at Eigenvalues and Eigenvectors
SFU MATH 232 3.2 Matrix and Linear Mappings
SFU MATH 232 4.6 Matrix of a Linear Mapping
SFU MATH 232 8.5 Singular Value Decomposition.
Комментарии
 0:23:02
0:23:02
 0:47:04
0:47:04
 0:39:48
0:39:48
 0:48:59
0:48:59
 0:34:02
0:34:02
 0:49:57
0:49:57
 0:43:32
0:43:32
 0:39:08
0:39:08
 0:57:35
0:57:35
 0:35:58
0:35:58
 0:42:43
0:42:43
 0:44:40
0:44:40
 1:07:56
1:07:56
 0:51:19
0:51:19
 0:41:42
0:41:42
 1:35:28
1:35:28
 1:06:44
1:06:44
 0:50:25
0:50:25
 0:45:50
0:45:50
 0:55:06
0:55:06
 0:56:01
0:56:01
 1:31:13
1:31:13
 0:42:50
0:42:50
 0:56:45
0:56:45