Structure of Atom Class 11 Chemistry - Shape of s Orbital

Structure of Atom Class 11 Chemistry - Shape of s Orbital

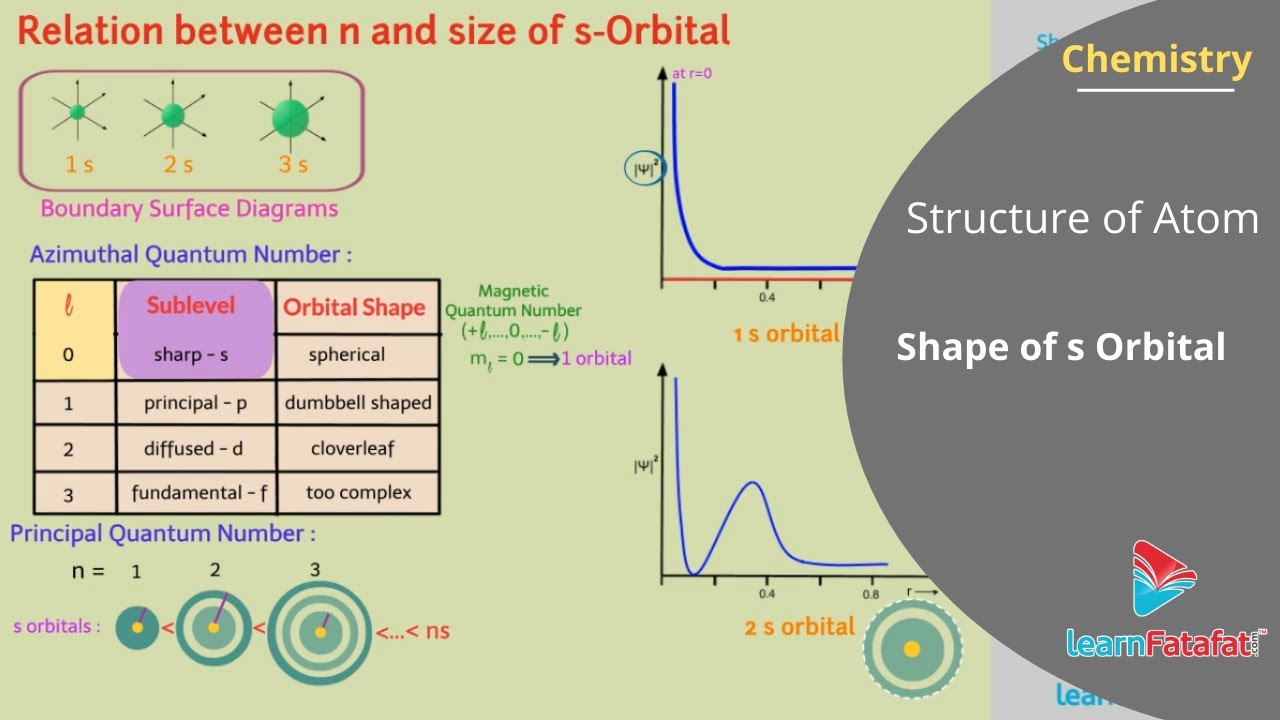
If Azimuthal quantum number l=0 then it suggests presence of s-orbital. Also if l=0 then it means magnetic quantum number ml=0 because ml can have value between +l, …, 0 ,…., -l. This suggests that s-subshell consists of only one orbital.
If we plot the graph of square of probability density as a function of distance r i.e. 𝛹2(r) for 1s orbital. Then it is observed that the probability density function is maximum at the nucleus and decrease sharply with increase in distance. this means that, the value of 𝛹2(r) depends on distance but independent of direction and hence the s-orbital must be spherically symmetrical about the nucleus. Therefore, it follows that the shape of s-orbital must be spherical.

Similarly for 2s-orbital, the probability density first decreases sharply to zero, then increases to some maximum value and again decreases. This means that the shape of 2s orbital is spherical and it is bigger than 1s orbital.
Dear students, with increase in value of principal quantum number ‘n’ i.e., size of s-orbitals increases.
Therefore size of s-orbitals increases in the order 1s ( 2s ( 3s ( …( ns. and distance of these orbitals from nucleus also increases.
Radial Nodes: The spherical surface where the probability density is zero is called spherical node or radial node. The number of spherical or radial nodes can be found by formula (n-l-1). e.g. for 1s orbital n=1 and l=0 therefore it has no spherical node. For 2s orbital n=2 and l=0 therefore it has one spherical node.
Nodal Planes: a plane passing through the nucleus on which the probability of finding electron is zero, is called a nodal plane. The number of nodal planes in any orbital is equal to azimuthal quantum number l. ∴ for s orbital, l=0 so, it does not have nodal plane.