Prove that the Square of any Odd Integer is Odd

Показать описание

Prove that the Square of any Odd Integer is Odd

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus Integration Insanity

Differential Equations Course

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)

Рекомендации по теме

Комментарии

Okay, my stats Professor told us to remember that you represent odd numbers with the expression 2N+1. That is because if N is an even number, then being multiplied by 2 doesn't change that, but adding 1 to it makes it odd. So I will use the expression 2N+1 to be my universally generalized ODD NUMBER. When we square that we get 4N^2+4N+1. Let's take that apart: in the first element whether N^2 is odd or even multiplying it by a factor of 2 makes it even. The same for the second expression, where whether N is odd or even multiplying it by a factor of 2 makes it even. Look at the last element of the SUM: BINGO! It's a 1 and if you add one to any sum of even numbers you will get an odd number. Since it is TRUE of a universal generality of for any Odd Number it is TRUE for every Odd Number.

leovolont

Odd n means that n ≡ 1 (mod 2) that is n^2 ≡ 1 (mod 2), QED.

raffaelevalente

Why do you say odd "integer?" Isn't an odd number an integer by definition? I'm just a Calculus 2 student, so please forgive my ignorance.

iamthebullSH

Try to speak in hindi it will more easy to understand because your English is

Kashishmalikk

Prove that the Square of any Odd Integer is Odd

Prove that the Square of any Odd Integer is Odd

How to prove that the square of an odd number is also odd - Melissa Maths

How To Prove The Quadratic Formula By Completing The Square

Can You Prove that one of these large numbers is not a perfect square?

direct proof 2: Prove that the product of perfect squares is a perfect square logic

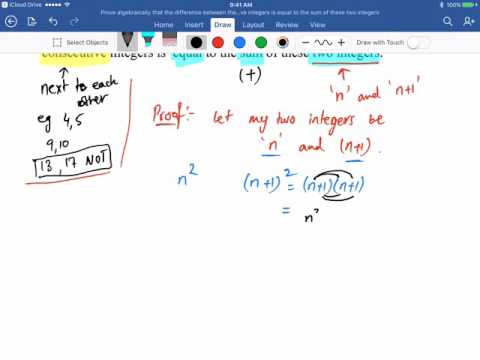
Prove algebraically that the difference between the squares of any two consecutive integers is equal

Prove that the there is No Rational Number Whose Square is 2

10th Std Maths Ex.2.1(5) Prove that square of any integer leaves the remainder either 0 or 1 when di

Unit 1 Pure Mathematics Trigonometry 5

Prove that the square of any positive integer is of the form 4q or 4q+1 for...|| Q.8 Ex.1.1 Class 10

Prove that sqrt(2) exists [ILIEKMATHPHYSICS]

How to prove the quadratic formula by completing squares

Prove that the square of any positive integer is of the form 5q, 5q+1, 5q+4 ...|| Q.9 Ex.1.1 Class10

Prove that the square of any positive integer of the form 5q+1 is ...|| Class 10 Ex.11 Q.6 RD SHARMA

How to prove any number irrational #shorts #mathshustle

sin square theta + cos square theta = 1 How to prove?

Prove by mathematical induction that the sum of squares of positive integers is n(n+1)(2n+1)/6

Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths

Prove A Number Irrational in 5 Seconds 🔥 #shorts #ytshorts #maths #class10maths

Prove that sum of the squares of the sides of a rhombus is equal to sum of the squares of diagonals

Prove that root 2 Is a rational number #solutions #realnumbers

direct proof 1: Prove the square of an integer is an integer

Prove that, in a right-angled triangle, the square of hypotenuse is equal to the sum of the squa...

Prove that sqrt(2) + sqrt(3) Cannot be a Rational Number