filmov
tv
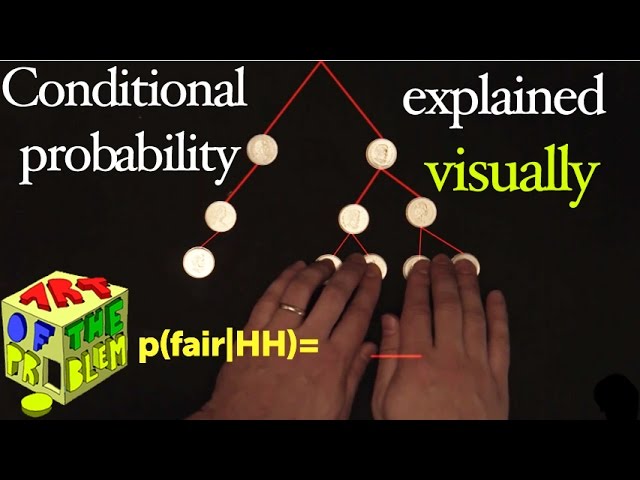
Conditional probability (Bayes' Theorem) explained visually
Показать описание
Visualize why evidence alters our confidence (probability) of prior events leading to Bayes theorem. This formula is explained using a tree analogy. This video acts as an introduction to Bayesian statistics.
Thanks a bunch to Kalid Azad for reviewing this lesson.
Thanks a bunch to Kalid Azad for reviewing this lesson.
Bayes' Theorem EXPLAINED with Examples
Conditional probability (Bayes' Theorem) explained visually
Bayes' Theorem - The Simplest Case
Bayes' Theorem of Probability With Tree Diagrams & Venn Diagrams
Bayes theorem, the geometry of changing beliefs
Bayes' Theorem, Clearly Explained!!!!
Tutorial 47- Bayes' Theorem| Conditional Probability- Machine Learning
Intro to Conditional Probability
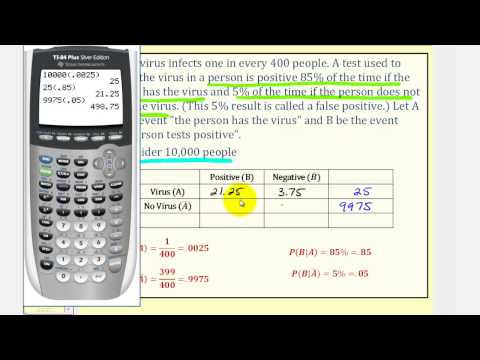
Conditional Probability: Bayes’ Theorem – Disease Testing (Table and Formula)
How to systematically approach truth - Bayes' rule
Probability - Conditional Probability and Bayes' Theorem
Conditional Probabilities, Clearly Explained!!!
Conditional Probability
Calculating conditional probability | Probability and Statistics | Khan Academy
Bayes Theorem Explained with Conditional Probability using Python | Bayesian Networks
Intro to Bayes’s Theorem | Probability Theory
Bayes' Theorem 1: Introduction and conditional probability
The Bayesian Trap
Conditional Probability With Venn Diagrams & Contingency Tables
Conditional Probability with Three Biased Coins Bayes Formula Application
Conditional Probability and Bayes' Theorem | Intro to Statistics
Probability: Bayes' Theorem
Conditional probability - Monty Hall problem
Bayes' Theorem Explained: A Simple Guide to Conditional Probability
Комментарии
 0:08:03
0:08:03
 0:05:06
0:05:06
 0:05:31
0:05:31
 0:19:14
0:19:14
 0:15:11
0:15:11
 0:14:00
0:14:00
 0:11:02
0:11:02
 0:06:14
0:06:14
 0:08:23
0:08:23
 0:19:08
0:19:08
 0:14:04
0:14:04
 0:10:56
0:10:56
 0:12:29
0:12:29
 0:06:43
0:06:43
 0:03:55
0:03:55
 0:12:41
0:12:41
 0:04:32
0:04:32
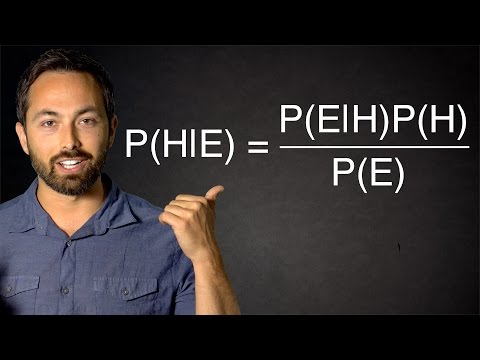 0:10:37
0:10:37
 0:16:26
0:16:26
 0:06:53
0:06:53
 0:08:28
0:08:28
 0:08:26
0:08:26
 0:06:08
0:06:08
 0:05:51
0:05:51