filmov
tv
How to find principal domain and principal solution of cotangent x (cot x)
Показать описание
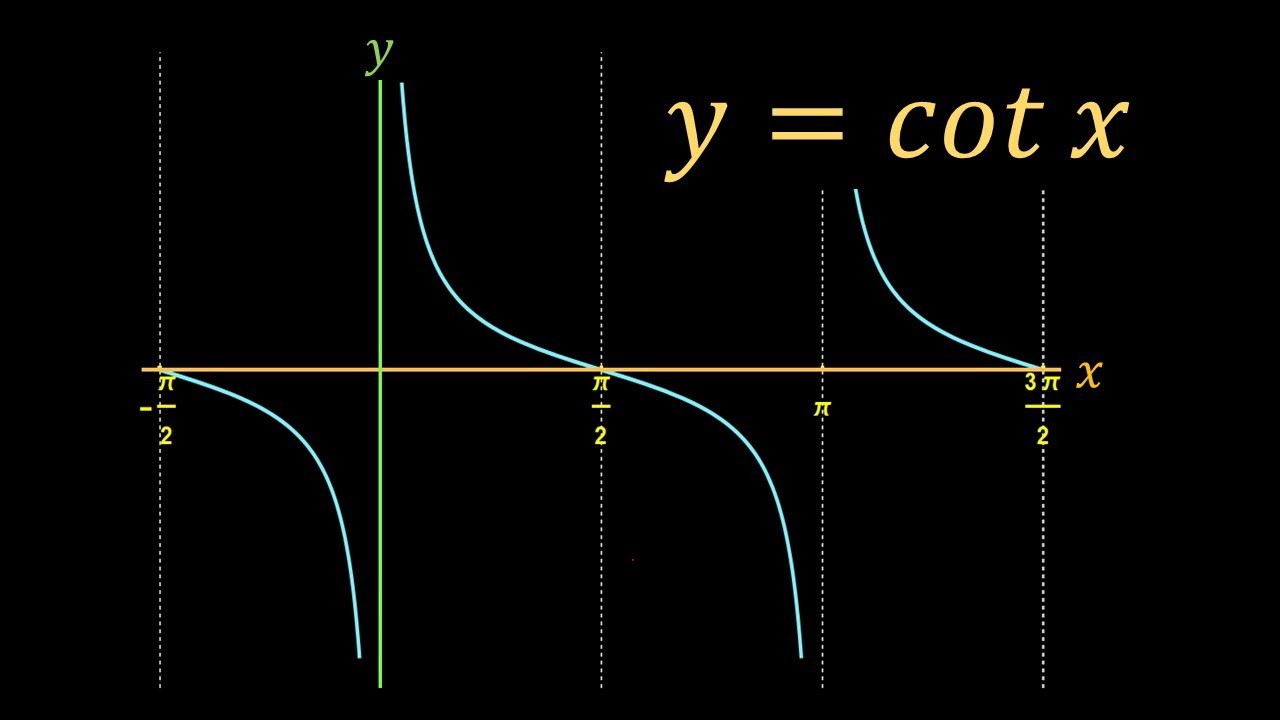
In this lecture, You will come to know how to find Principal Domain and Principal Solution of cotangent x (cot x), which is very essential while solving trigonometric equations. This concept is also useful to find domain and range of inverse trigonometric functions. First I have explained about domain and range of cot x then by using domain of this function, I have tried to convince you that which conditions must be kept in mind to choose principal domain of trigonometric Ratios. I have explained this concept by using three necessary and sufficient conditions of principal domain, which are given below:-
(a) Function must be one-to-one or bijective.
(b) it must be near origin.
(c) It must cover its full range of values.
Principal solution is the value of unknown angle belonging to the principal domain of trigonometric function. It is numerically the least value of the angle. The principal domain for a trigonometric function is defined as an interval belonging to the domain of said function in which it is bijective i.e., strictly monotonic and takes up all possible values, conventionally. It is considered nearest to the origin preferable positive.
(a) Function must be one-to-one or bijective.
(b) it must be near origin.
(c) It must cover its full range of values.
Principal solution is the value of unknown angle belonging to the principal domain of trigonometric function. It is numerically the least value of the angle. The principal domain for a trigonometric function is defined as an interval belonging to the domain of said function in which it is bijective i.e., strictly monotonic and takes up all possible values, conventionally. It is considered nearest to the origin preferable positive.
 0:04:51
0:04:51
 0:01:56
0:01:56
 0:03:17
0:03:17
 0:06:54
0:06:54
 0:03:43
0:03:43
 0:00:56
0:00:56
 0:06:42
0:06:42
 0:22:47
0:22:47
 0:04:01
0:04:01
 0:03:53
0:03:53
 0:07:47
0:07:47
 0:24:47
0:24:47
 0:00:06
0:00:06
 0:04:05
0:04:05
 0:00:47
0:00:47
 0:01:34
0:01:34
 0:27:04
0:27:04
 0:07:56
0:07:56
 0:05:16
0:05:16
 0:03:23
0:03:23
 0:03:24
0:03:24
 0:00:16
0:00:16
 0:00:38
0:00:38
 0:06:44
0:06:44