filmov
tv
Calculating the Determinant | Extension of The Essence of Linear Algebra #SoME2

Показать описание
Thanks for watching, this was made in only 7 days and is my first time using basically everything that helped create everything you see in it from the animations, to the editor. It was pretty tough to do, but fun none the less. Just don't expect Hollywood quality anything from it.
This was produced for the Summer of Math Exposition 2 which is a competition designed by @3Blue1Brown
A quick side note, at 4:30 in the video I misspoke, I said "the determinants b times d term" instead of "the determinants b times c term". I was saying so many letters all day I guess that one got past me.
Here is a link to chapter 6 of the essence of Linear Algebra I referenced
This was produced for the Summer of Math Exposition 2 which is a competition designed by @3Blue1Brown
A quick side note, at 4:30 in the video I misspoke, I said "the determinants b times d term" instead of "the determinants b times c term". I was saying so many letters all day I guess that one got past me.
Here is a link to chapter 6 of the essence of Linear Algebra I referenced
Calculating the Determinant | Extension of The Essence of Linear Algebra #SoME2
Sarrus Rule | How To Fast Calculate The Determinant of A 3 x 3 Matrix | Linear Algebra
Chapter 11 Extension: Finding Determinants
The Determinant of a 4 by 4 Matrix Using Cofactor Expansion (Expansion by Minors)
Determinants
Determinants in Geometric Algebra
Expansion of Determinant by Rows & Columns
n x n determinant | Matrix transformations | Linear Algebra | Khan Academy
Calculating the Determinant
Theorem: Determinant of a Product of Matrices
Determinants - Intro 1/3
Solution 80: Slaying a Monstrous Determinant using Second Differences
Calculating Torques with a Determinant
Fredholm Determinants of Connection Graphs
Pre-Calculus 8.4: The Determinant of a Square Matrix part 1
How To Find The Determinant of a 3x3 Matrix and a 4x4 Matrix #matrix #determinants
Determinant of Matrix by Cross Multiplication_Shortcut Method_Casio fx-991ES Calculator Proof
Linear Algebra in C++ - Part 3 - NxN Matrix Determinant
Calculating Determinants 4x4 (Example 2)
How to find the determinant of a 3 by 3 matrix (3 ways) linear algebra tutorial
The Determinant - Part 1
Determinants as Areas or Volumes
10.6 Determinants
Determinant Formula for Volume of n-Parallelotope
Комментарии
 0:02:04
0:02:04
 0:02:36
0:02:36
 0:06:33
0:06:33
 0:06:39
0:06:39
 0:00:58
0:00:58
 0:10:08
0:10:08
 0:18:40
0:18:40
 0:06:08
0:06:08
 0:08:21
0:08:21
 0:10:57
0:10:57
 0:13:41
0:13:41
 0:09:14
0:09:14
 0:12:49
0:12:49
 0:09:19
0:09:19
 0:08:31
0:08:31
 0:03:42
0:03:42
 0:23:12
0:23:12
 0:21:45
0:21:45
 0:14:57
0:14:57
 0:25:41
0:25:41
 0:05:36
0:05:36
 0:13:40
0:13:40
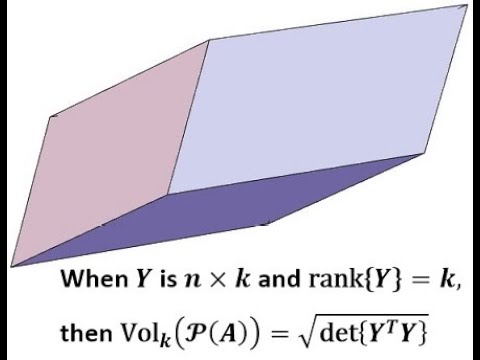 0:12:41
0:12:41