filmov
tv
Найдите периметр треугольника

Показать описание
Решаем задачу, опираясь на теорему о том, что биссектрисы внутреннего и двух внешних углов треугольника пересекаются в одной точке.
Периметр треугольника. Как найти периметр треугольника?...
Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсам...
ПЕРИМЕТР ТРЕУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэ...
Периметр треугольника
КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 класс...
Найдите периметр треугольника
Как вычислить периметр #геометрия #задача #треугольник #периметр...
Найти периметр треугольника
Площадь треугольника. Как найти площадь треугольника?
Периметр треугольника
Хитрый периметр
Что такое периметр. Как найти периметр многоугольника?
№566. Точки Р и Q — середины сторон АВ и АС треугольника ABC. Найдите периметр треугольника...
Запомни: все формулы для площади треугольника
Как найти периметр?
Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | Алгебра...
Как найти площадь треугольника без формулы?
Найдите площадь треугольника на рисунке ★ Два способа решения...
Математика 2 класс. «Периметр треугольника, прямоугольника и квадрата»...
№564. Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника,...
Решение задачи №1 из ЕГЭ математика
Задача 6 №27624 ЕГЭ по математике. Урок 71
№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр...
№91. Периметр треугольника равен 48 см, а одна из сторон равна 18 см. Найдите две другие...
Комментарии
 0:05:14
0:05:14
 0:01:22
0:01:22
 0:00:59
0:00:59
 0:01:10
0:01:10
 0:01:19
0:01:19
 0:07:47
0:07:47
 0:00:35
0:00:35
 0:00:57
0:00:57
 0:08:02
0:08:02
 0:00:18
0:00:18
 0:00:47
0:00:47
 0:05:42
0:05:42
 0:02:13
0:02:13
 0:00:52
0:00:52
 0:01:05
0:01:05
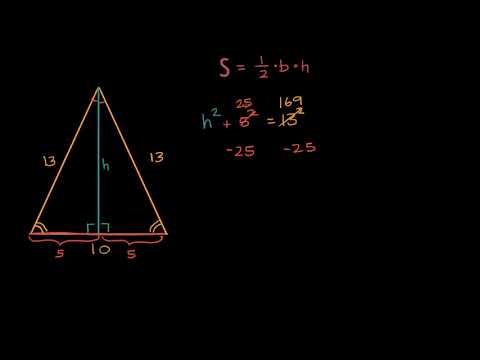 0:03:35
0:03:35
 0:01:32
0:01:32
 0:06:33
0:06:33
 0:15:39
0:15:39
 0:01:45
0:01:45
 0:05:20
0:05:20
 0:01:36
0:01:36
 0:01:01
0:01:01
 0:02:27
0:02:27