huffman coding greedy algorithm text compression

huffman coding: a greedy algorithm for text compression

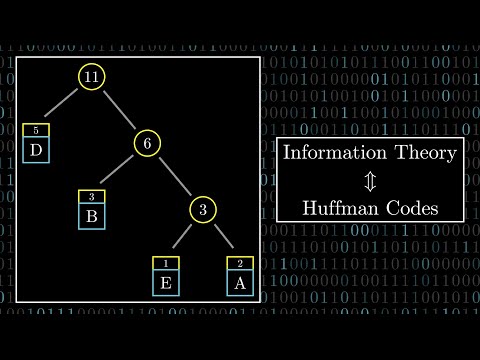
huffman coding is a widely used method for lossless data compression. it works by assigning variable-length codes to input characters, with shorter codes assigned to more frequently occurring characters. the algorithm is greedy because it builds the optimal prefix code based on the frequencies of characters.

steps of huffman coding

1. **frequency count**: count the frequency of each character in the input text.
2. **build a min-heap**: create a min-heap (or priority queue) with each character as a node, where the key is the frequency of the character.
3. **create huffman tree**:
- while there is more than one node in the heap:
- extract the two nodes with the smallest frequency.
- create a new internal node with these two nodes as children and a frequency equal to the sum of their frequencies.
- insert this new node back into the heap.
4. **generate codes**: traverse the huffman tree to assign codes to each character. typically, a left edge is represented by '0' and a right edge by '1'.
5. **encode the input**: replace each character in the input with its corresponding huffman code.
6. **decode the input**: reverse the encoding process using the huffman tree.

example code in python

here is a complete implementation of huffman coding in python:

explanation of the code

1. **node class**: represents a node in the huffman tree. each node has a character, its frequency, and pointers to left and right children.
2. **frequency count**: a defaultdict is used to count the occurrences of each character in the input text.
3. **min-heap**: a list of `node` instances is created and transformed into a min-heap using `heapq`.
4. **huffman tree construction**: nodes with the smallest frequencies are merged iteratively until only one node remains (the root of the huffman tree).
5. **code generation**: a recursive function generates the binary codes by traversing the tree.
6. **encoding and decodin ...

#HuffmanCoding #GreedyAlgorithm #python
Huffman coding
greedy algorithm
text compression
data compression
variable length coding
binary tree
optimal prefix codes
lossless compression
entropy encoding
frequency analysis
algorithm efficiency
symbol encoding
coding tree
compression ratio
data representation