filmov
tv
Awesome Olympiad Problem For Maths Genius 😍| Aman Malik Sir

Показать описание
This question is for all maths genius and maths lovers.
If aabb=x^2, Find x
This is a very amazing question from Maths Olympiad which will surely test your mathematics skills and critical thinking.
You'll not be able to directly implement the direct mathematics fundamentals rather there will be critical points you need to think about from the core maths perspective.
Solving such questions will also train your mind to open up and go for in-depth critical thinking.
Maths Olympiad problems are surely a must-do thing for you if you want to develop such skills.
Stay tuned with @BHANNATMATHS for more such interesting questions.
🚀🚀Social Media Links:🚀🚀
----------------------------------------------------------------------------------------
Telegram Handle: @bhannatmaths @bhannatmathsofficial
----------------------------------------------------------------------------------------
Credits:
Music: Dark Water by Soundridemusic
#maths #mathematics #olympiads #amansirmaths #jee #jeemains #iitjee #jeeadvanced #olympiadmath #mathsolympiad
If aabb=x^2, Find x
This is a very amazing question from Maths Olympiad which will surely test your mathematics skills and critical thinking.
You'll not be able to directly implement the direct mathematics fundamentals rather there will be critical points you need to think about from the core maths perspective.
Solving such questions will also train your mind to open up and go for in-depth critical thinking.
Maths Olympiad problems are surely a must-do thing for you if you want to develop such skills.
Stay tuned with @BHANNATMATHS for more such interesting questions.
🚀🚀Social Media Links:🚀🚀
----------------------------------------------------------------------------------------
Telegram Handle: @bhannatmaths @bhannatmathsofficial
----------------------------------------------------------------------------------------
Credits:
Music: Dark Water by Soundridemusic
#maths #mathematics #olympiads #amansirmaths #jee #jeemains #iitjee #jeeadvanced #olympiadmath #mathsolympiad
Комментарии
 0:11:56
0:11:56
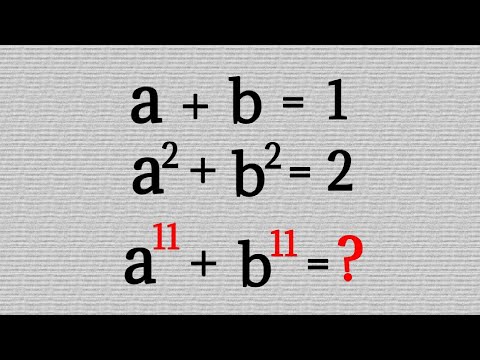 0:13:03
0:13:03
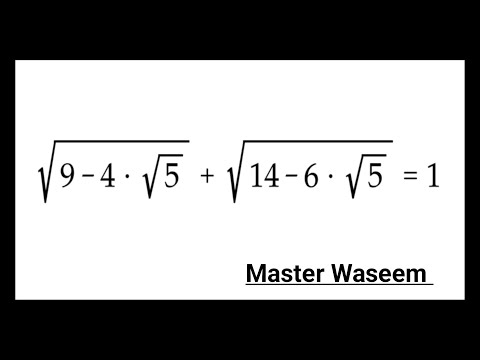 0:02:56
0:02:56
 0:00:52
0:00:52
 0:02:51
0:02:51
 0:10:38
0:10:38
 0:10:55
0:10:55
 0:08:41
0:08:41
 0:14:22
0:14:22
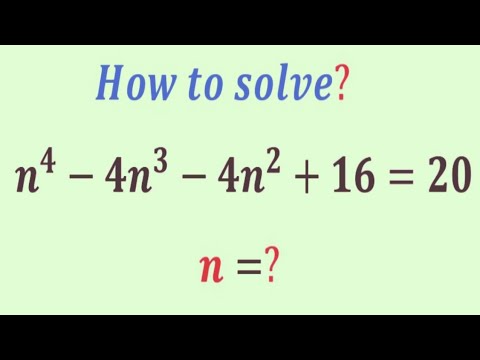 0:11:50
0:11:50
 0:08:08
0:08:08
 0:25:44
0:25:44
 0:13:51
0:13:51
 0:03:21
0:03:21
 0:10:55
0:10:55
 0:14:40
0:14:40
 0:07:38
0:07:38
 0:13:36
0:13:36
 0:09:02
0:09:02
 0:16:58
0:16:58
 0:08:47
0:08:47
 0:00:33
0:00:33
 0:02:34
0:02:34
 0:00:28
0:00:28