Fractional differentiation and integration: Theories, methods, and applications w/ Prof Dr Atangana

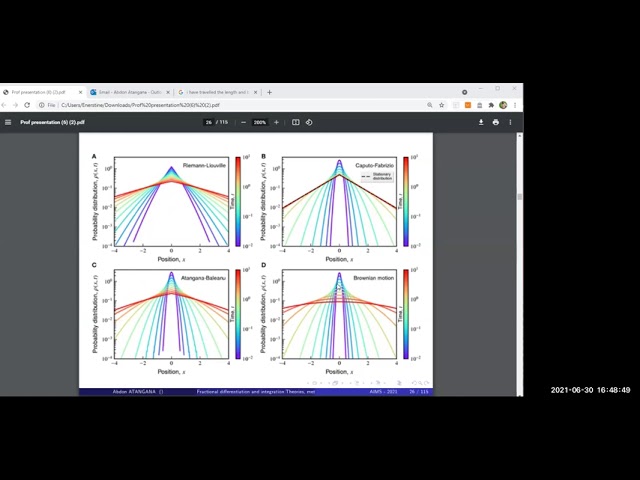
Classical differential and integral operators have been used in model processes observed in real-world problems. However, in many cases when comparing these models with experimental data, one observed a significant disagreement between experimental data and the mathematical models. A clear indication that classical differential and integral operators have failed to capture the complexities of nature. Initiated from a discussion by L ' Hopital and Leibniz, developed by Riemann, Liouville, Cauchy, Abel and many more imminent mathematicians and founders of classical calculus, the notion of fractional differentiation and integration was introduced and used in many real-world problems with great success. This talk is devoted to a discussion underpinning, the theory, methods, and applications of fractional differential operators.

Keywords: Power law, exponential decay, Mittag-Leffler function, applications

[enelderuisseau]

Hello,
I am a student in thesis of mathematics.

Thank you for this presentation. I have a question for professor atangana. In the definition of the fractional derivative of caputo. If we use the definition of the convolution product, what condition should we have on the function u or on the kernel to have the bounds 0 to t in the integral of the definition without convolution?

[chernettuge]

What can be said about fractional derivatives in Partial differential equations?