Introduction to the Doppler effect: animations with sound, Doppler effect derivations and examples.

Показать описание

00:00 In this introduction to the Doppler effect, we start with a qualitative introduction to the Doppler effect using animations with sound in the "moving listener" Doppler effect and the "moving source" Doppler effect. The video is split into three main parts including the Doppler effect derivations in the "moving listener" case, the "moving source" case, and the general case in which the listener and source may both be moving. In each section, we follow the derivation of the Doppler effect equations with two examples illustrating how to apply the Doppler formulas, so the video includes six worked examples of the Doppler effect.

02:51 Moving Listener Case: We derive the Doppler effect equation for the case of a stationary source emitting a tone and a moving listener. The main idea of the derivation is that the wavelength of the sound waves can be quickly determined by using the wave speed formula v=f*lambda. Then we get the relative velocity between the sound waves and the listener. Next we use the relative velocity to compute the time it takes the listener to cross from crest to crest across the sound waves. The reciprocal of this time is the frequency heard by the listener.

05:19 Moving Listener Examples: We apply our new Doppler effect equation to two examples where a listener approaches a sound source, then the listener passes the sound source and heads away from it. We include an animation with sound to illustrate the frequencies heard by the listener, including the transition at which the frequency shifts from high to low as the listener passes the sound source.

07:00 Moving Source Case: We derive the Doppler effect equation for the case in which the source is moving and the listener is stationary. As the source moves, the sound waves are compressed in the forward direction and rarefied in the direction opposite the motion of the source. The compression can be understood by seeing that the source moves a little bit between the emission of wave crests. We calculate this small shift and use it to determine the slightly shorter wavelength of the sound waves due to the motion of the source. Finally, we use that shorter wavelength to determine the frequency heard by the listener.

09:18 Moving Source Examples: We work two Doppler shift examples for the case of a moving source. In the examples, a car emitting a 440Hz tone approaches the listener. Then the car passes the listener. As the car approaches the listener, we hear a higher tone given by the Doppler effect equation. As the car moves away from the listener, we hear a lower tone. We include the transition where the sound frequency changes from high to low as the car passes the listener.

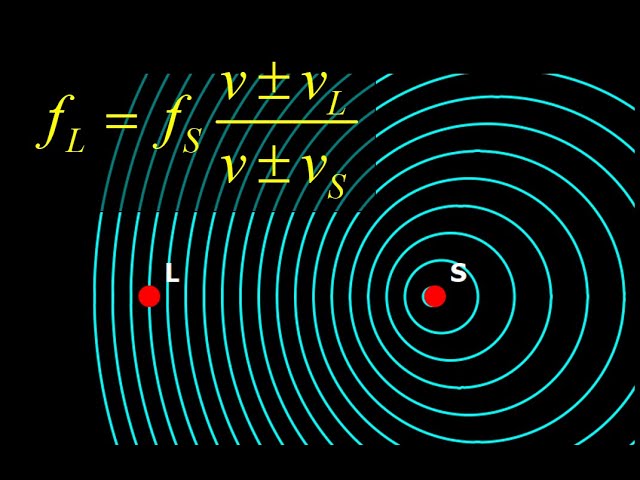
10:54 General Case - Listener and Source Both Moving: Finally, we derive the general Doppler effect formula f_L=f_s*(v+/-v_L)/(v+/-v_s). We discuss how to pick the plus and minus signs in the Doppler formula. In the Doppler effect equation, we pick the sign of the listener's velocity to result in the correct qualitative behavior: increasing the frequency if the listener moves toward the source, and vice versa. We pick the sign of the velocity of the sound source using the same kind of reasoning, but taking care to pick the minus sign if the frequency should increase (because a smaller denominator yields a larger result).

13:02 Listener and Source Both Moving Examples: Last two examples of the Doppler effect: we work two examples in which both the sound source and the listener are moving. We carefully pick the signs in the Doppler formula and computed the shifted frequencies when both objects are moving, and we're done!