filmov
tv
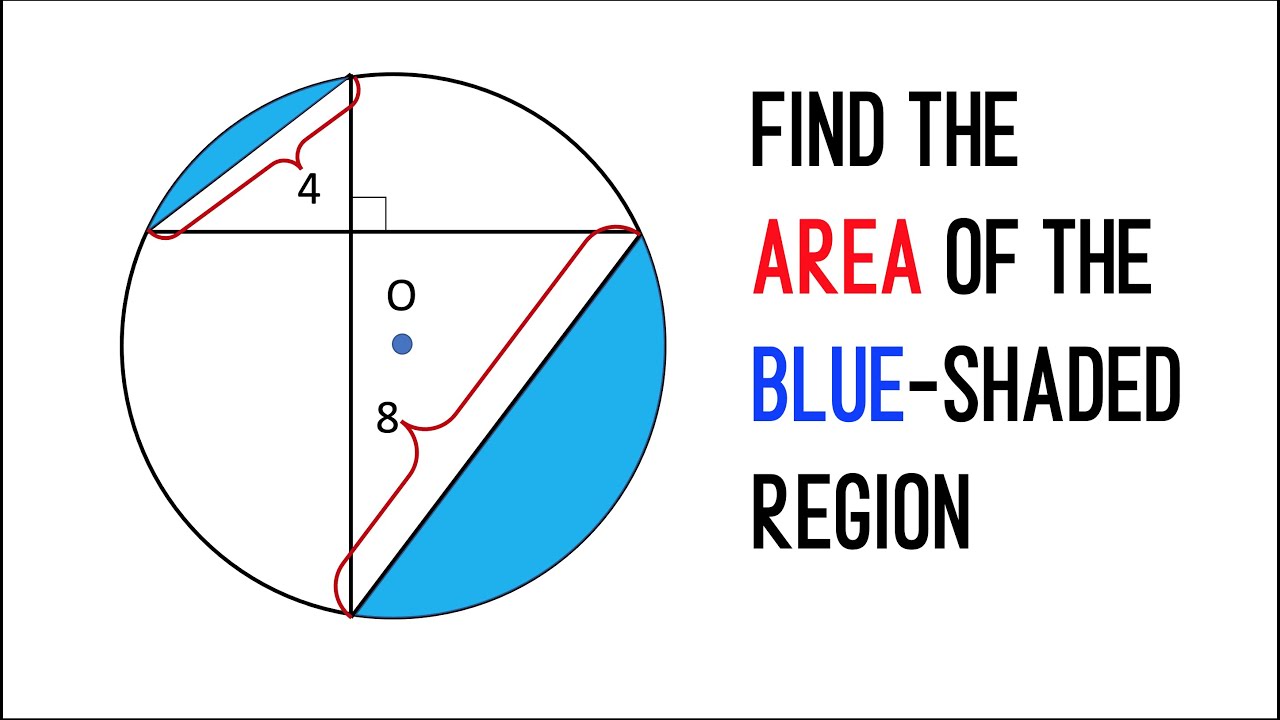
Find area of blue shaded region in a circle Given the Length of Chords | An Elegant Geometry Problem
Показать описание
In this problem, we are given a circle with two chords of length 4 and 8 units. Our goal is to find the area of the blue shaded region in the circle.
To solve this problem, we will be using two main key concepts: the Inscribed Angle Theorem, the Pythagorean Theorem.
Firstly, let's recall the Inscribed Angle Theorem. This theorem states that an angle formed by two chords in a circle is half the measure of the intercepted arc. This means that if we can find the measure of the intercepted arc, we can use it to calculate the measure of the inscribed angle.
Next, we will use the Pythagorean Theorem. This theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. We will use this theorem to find the length of the radius of the circle.
To solve this problem, we will be using two main key concepts: the Inscribed Angle Theorem, the Pythagorean Theorem.
Firstly, let's recall the Inscribed Angle Theorem. This theorem states that an angle formed by two chords in a circle is half the measure of the intercepted arc. This means that if we can find the measure of the intercepted arc, we can use it to calculate the measure of the inscribed angle.
Next, we will use the Pythagorean Theorem. This theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. We will use this theorem to find the length of the radius of the circle.
0:09:09
0:06:21
0:03:15
0:08:09
0:08:02
0:09:22
0:06:49
0:09:15
0:08:10
0:10:14
0:05:35
0:08:36
0:00:31
0:02:29
0:05:53
0:04:50
0:06:10
0:08:53
0:15:22
0:08:16
0:04:48
0:08:47
0:05:58
0:09:52