filmov
tv
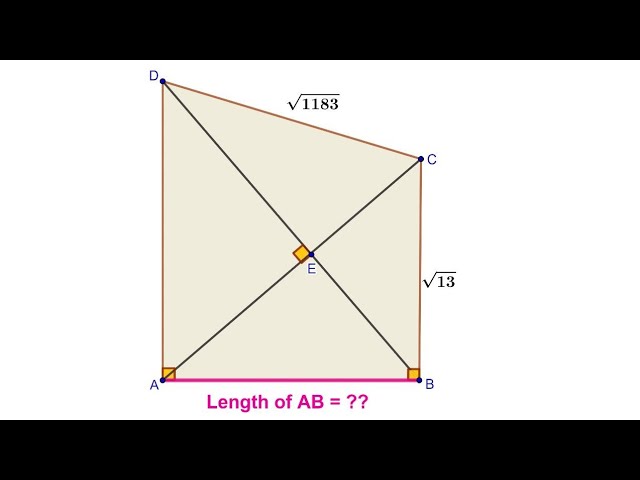
Find the length of side AB of a trapezium ABCD. | DA⊥AB, CB⊥AB, AC ⊥ BD, BC = √13 ; CD = √1183.
Показать описание
In this video tutorial, we will learn how to find the unknown side AB of a given trapezium ABCD (Trapezoid). We are given the lengths of two sides, BC = √13 and CD = √1183. Sides BC and AB are perpendicular, DA and AB are perpendicular. Diagonals AC and BD are mutually perpendicular.
#Similarity_in_right_triangles
#Pythagorean_Theorem
#Geometric_Mean
Useful for :
#NTSE, #GRE, #IITJEE, #IOQM, #RMO, #INMO, #ISI, #CMI, #MAT, #CAT, #SAT, #BITSAT, #PET, #CET, #MCA, #NDA, #CDS, #SSC, #KVPY, #RRB, #PO, etc
#Similarity_in_right_triangles
#Pythagorean_Theorem
#Geometric_Mean
Useful for :
#NTSE, #GRE, #IITJEE, #IOQM, #RMO, #INMO, #ISI, #CMI, #MAT, #CAT, #SAT, #BITSAT, #PET, #CET, #MCA, #NDA, #CDS, #SSC, #KVPY, #RRB, #PO, etc
How To Calculate The Missing Side Length of a Triangle
Using the sine function to find the missing length of the hypotenuse
How to Find the Missing Side Length of a Rectangle when you know the Area
Find Missing Side Length with Only an Angle and One other Side
Given the triangle, Find the length of side x using the Law of Sines
Find the length of one side if area is 576cm² of square | Aptitude Test |Rk Learning
Find the Length of a Missing Side of a Right Triangle and Perimeter and Area
Find Missing Side Length Using SohCahToa Trig in Geometry
Low Back and Hip Relief : Stretch Therapy for 50+
Find the Missing Side Length in a Rectangular Prism, when you know the volume
Calculate the Length of the Side of the Square ABCD | Step-by-Step Explanation
Math Olympiad | Find missing side length X of the triangle | (Centroid and Medians) | #math #maths
Finding Perimeter when a Side Length is Missing (Composite Figures) | Math with Mr. J
Side Length of a Square from Perimeter
Use Tangent to Determine The Length of an Adjacent Side of a Right Triangle
How to find unknown side length using Pythagorean theorem 2.1 gr 9 applied
Find Side Length X of this Quadrilateral | Fast & Easy Tutorial
Find Possible Lengths of Third Side in a Triangle
Pythagorean Theorem: A Step-by-Step Guide | Find a Missing Side Length Using the Pythagorean Theorem
Find The Length of unknown side
Ex 1: Find the Length of a Side of a Triangle Using Similar Triangles
How to find the missing length of a leg of a right triangle
Find Missing Side Length Of Cube Given Its Surface Area
Use the Law of Sines to Determine a Side Length (AAS)
Комментарии
 0:29:56
0:29:56
 0:04:55
0:04:55
 0:04:26
0:04:26
 0:00:59
0:00:59
 0:01:08
0:01:08
 0:06:22
0:06:22
 0:05:45
0:05:45
 0:00:48
0:00:48
 0:33:56
0:33:56
 0:02:38
0:02:38
 0:08:08
0:08:08
 0:08:09
0:08:09
 0:05:17
0:05:17
 0:01:41
0:01:41
 0:03:27
0:03:27
 0:02:25
0:02:25
 0:06:07
0:06:07
 0:03:02
0:03:02
 0:13:52
0:13:52
 0:03:12
0:03:12
 0:03:01
0:03:01
 0:02:45
0:02:45
 0:03:01
0:03:01
 0:03:55
0:03:55