Exponential Functions Complete Test IB MCR3U

#exponentialfunctions_Test #mcr3u_functions #anilkumar #globalmathinstitute #olevel_mathematics #olevelmathematics
Q1. Simplify: (9^(4x+3y) )(81^(2x-4y) )
Q2. Simplify: (36√x-x^(3/2))/(√x-6)
Q3. Simplify: (x^2 y+x^4 y^3 )^4/(x^5 y^7 )
Q4. Solve for x and verify your solution: 9^(1/4) (1/3)^(x/2)=∛(27^4 )
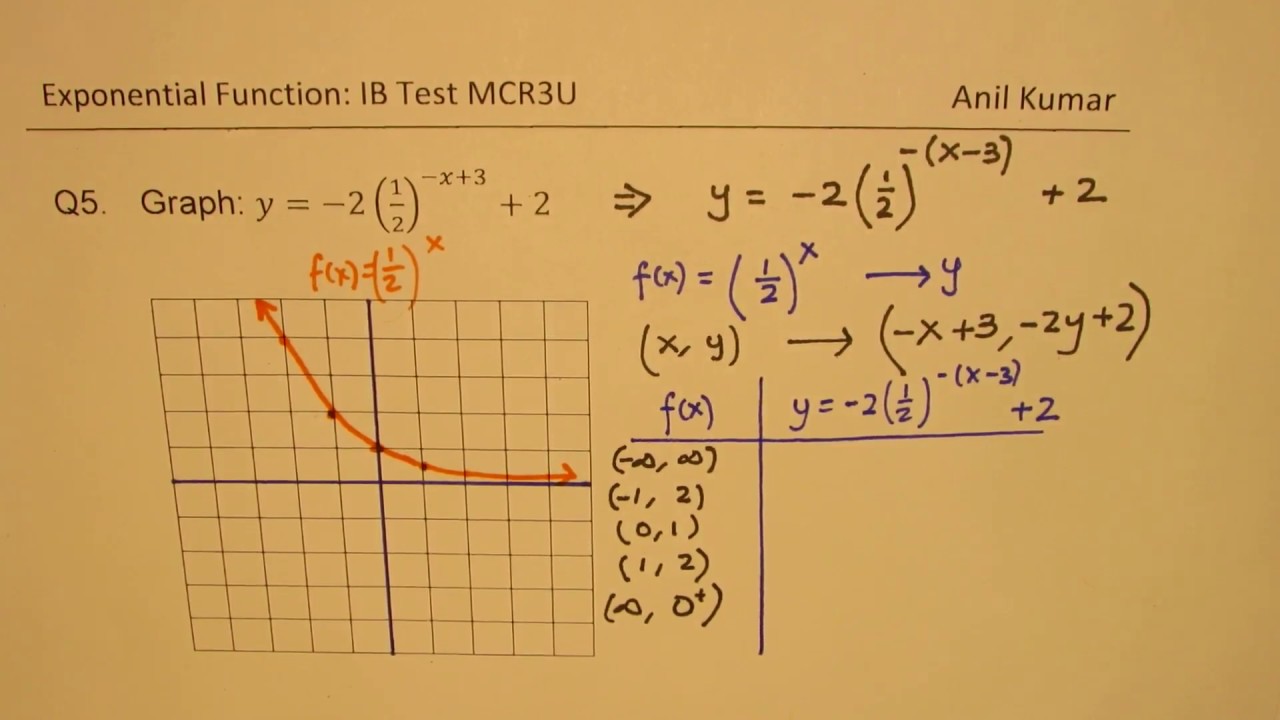
Q5. Graph: y=-2(1/2)^(-x+3)+2
Q6. State the transformations necessary to transform
f(x)=(2)^(x+1)+2 to g(x)=(1/4)^(1/2 x-1/4)-1
Q7. Anil baked a cake and left it on the counter to cool. An equation that models this situation is T(t)=70(e)^((-t)/10)+14 where T is the temperature in degrees Celsius and t is the time elapsed in minutes.
a. This example is of exponential growth or decay.
b. What is the temperature of the cake when it is first removed from the oven?
c. What is the air temperature in the room where the cake has been left to cool?
d. How long will it take for the temperature of the cake to drop to 35˚C?
Q8. After 28 hours a sample of Phosperium-1980 decayed to 1/128 of its original mass. Determine its half life.

Q9. A shade allows light to pass through from a lamp, but reduces the intensity of the light. The intensity of the light is reduced by 15% if the fabric is 1 mm thick. Each additional millimetre of fabric reduces the intensity by another 15%.
a. Write an expression that gives percent, P, of light which penetrates x mm of fabric.
b. Use the equation above to determine the percentage of light that will pass through a cloth that is 2.75 mm thick.
Q10. In 1950, the world population was approximately 2.5 billion. The population doubled to 5 billion in 1987.

a. What was the average annual growth rate of the world population from 1950 to 1987?
b. If the growth continued at the same rate, what should be the population in 2020?

Q11. The graph of the function f(x)=a(2)^x+b with y-intercept at 8 passes through the point (2, 20). Find the value of a + b.

Q12. Solve for x and y: 4^x×2^y=16 and 8^x=2^(y/2) #GCSE #SAT #EQAO #IBSLmath