filmov
tv
CMO (Canadian Mathematic Olympiad) 1969, #5

Показать описание
Today's question is "In triangle ABC, CD is the bisector of the angle ACB, prove that (2ab x cos(c/2))/(a+b)=d"-- CMO 1969, #5
Please comment below if you have any questions or any other math problems you would like to share!
The Questions Anna Came Across
I am 14 and I hope I can help more people with math and I hope more people like math!!
Anna Muyan Li
Please comment below if you have any questions or any other math problems you would like to share!
The Questions Anna Came Across
I am 14 and I hope I can help more people with math and I hope more people like math!!
Anna Muyan Li
CMO (Canadian Mathematic Olympiad) 1969, #5
hard Canadian mathematical Olympiad 1969
Olympiad Right Triangle Inequality (Canada 1969 - visual proof)
hard canadian Mathematical Olympiad
Canadian Math Olympiad Q1 Solution - Contradict the Contradiction
Canadian Mathematical Olympiad, problem 1, 2018 - part 1
canadian Mathematical Olympiad
COMC Practice Problems -- Week 01 Prob B -- 2019
Canadian Mathematical Olympiad, 2018, problem 1 - part 2
COMC Practice Problems -- Week 01 Prob A -- 2019
Canadian mathematical Olympiad
COMC Practice Problems -- Week 06 -- 2019
COMC Practice Problems -- Week 02 -- 2019
COMC Practice Problems -- Week 04 -- 2019
COMC Practice Problems -- Week 07 -- 2019
COMC Practice Problems -- Week 03 -- 2019
COMC Practice Problems -- Week 05 -- 2019
Top 20 Country by International Mathematical Olympiad Gold Medal (1959-2019)
A Physics Prof Bet Me $10,000 I'm Wrong
Number of integral solutions (Interesting application of Combinatorics)
MATH299B Video #1 - Functional Equation from Putnam Exam
Maths Olympiad: Number theory: p-adic variation of n! formula proof Vp(n!)=n-Sp(n)/p-1 with example
INTERNATIONAL MATHEMATICAL OLYMPIAD 1961
Zeller's Congruence | The Day of the Week
Комментарии
 0:02:43
0:02:43
 0:13:53
0:13:53
 0:01:38
0:01:38
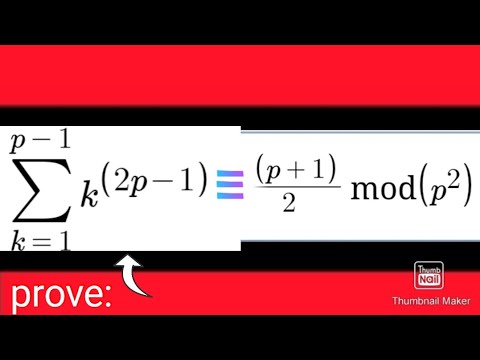 0:10:50
0:10:50
 0:06:43
0:06:43
 0:12:56
0:12:56
 0:04:37
0:04:37
 0:30:50
0:30:50
 0:10:17
0:10:17
 0:25:15
0:25:15
 0:06:26
0:06:26
 0:42:44
0:42:44
 1:00:18
1:00:18
 0:31:06
0:31:06
 0:46:02
0:46:02
 0:33:44
0:33:44
 1:03:52
1:03:52
 0:02:21
0:02:21
 0:17:56
0:17:56
 0:10:18
0:10:18
 0:11:07
0:11:07
 0:09:03
0:09:03
 0:05:23
0:05:23
 0:03:38
0:03:38