filmov
tv
Tom Kennedy: Renormalization group maps for Ising models and tensor networks (December 9, 2021)
Показать описание
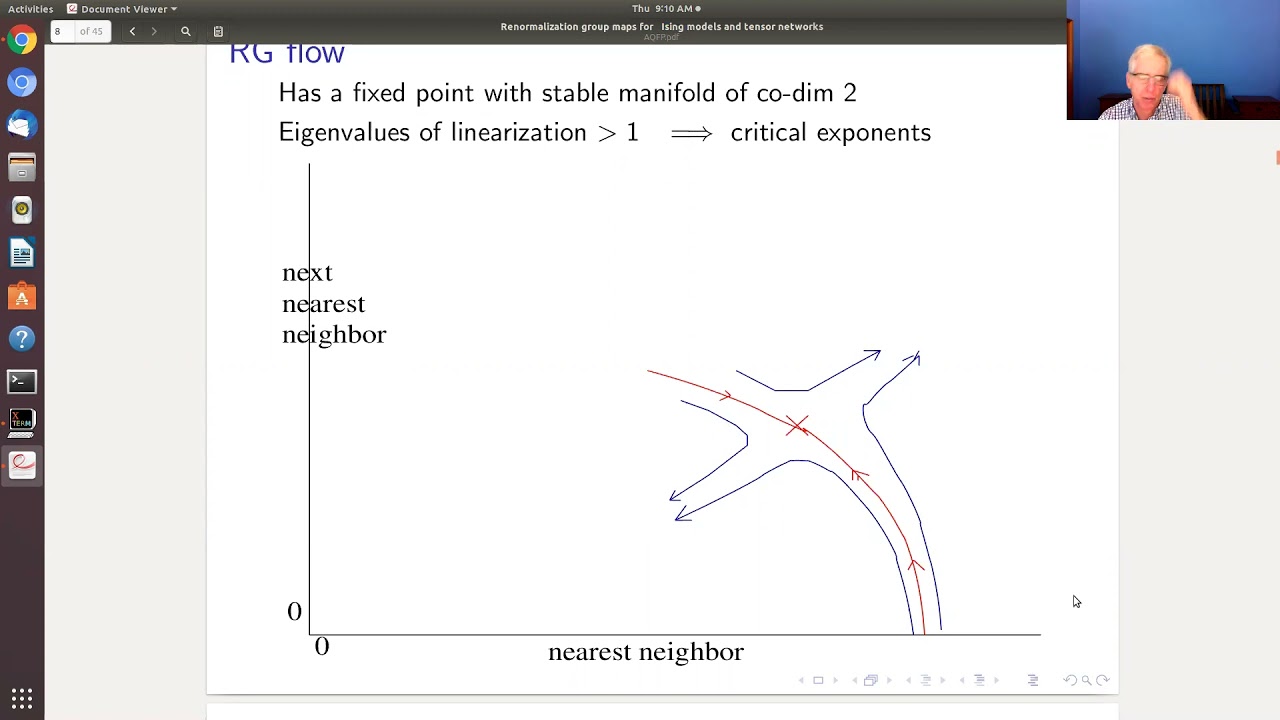
We will briefly review Wilson-Kadanoff type renormalization group (RG) maps for Ising spin systems and the lack of progress in proving that there is a non-trivial fixed point for these maps. (These maps are also known as real-space RG transformations.) The Ising model can be written as a tensor network, and RG maps can be defined in the tensor network formalism. Numerical studies of such RG maps have been quite successful at reproducing the known critical behavior in two dimensions. In joint work with Slava Rychkov we proved that in two dimensions for a particular tensor network RG map the high temperature fixed point is locally stable, i.e., there is a neighborhood of the high temperature fixed point such that for an initial tensor in this neighborhood, the iterations of the RG map converge to the high temperature fixed point. We hope that this is a modest first step towards proving the existence of a non-trivial fixed point for a tensor network RG map which would correspond to the critical point of the Ising model.
 1:10:08
1:10:08
 1:20:10
1:20:10
 1:36:41
1:36:41
 0:56:51
0:56:51
 0:44:25
0:44:25
 2:26:05
2:26:05
 0:25:41
0:25:41
 1:21:52
1:21:52
 0:51:48
0:51:48
 0:55:37
0:55:37
 1:16:09
1:16:09
 0:45:26
0:45:26
 0:45:30
0:45:30
 1:05:34
1:05:34
 0:01:08
0:01:08
 0:22:34
0:22:34
 0:35:48
0:35:48
 0:28:39
0:28:39
 1:09:28
1:09:28
 0:31:22
0:31:22
 1:02:12
1:02:12
 1:23:44
1:23:44
 0:30:16
0:30:16
 1:13:00
1:13:00