filmov
tv
Converting iterated integrals to polar coordinates (KristaKingMath)

Показать описание
Learn how to convert iterated integrals from cartesian coordinates to polar coordinates.
● ● ● GET EXTRA HELP ● ● ●
● ● ● CONNECT WITH KRISTA ● ● ●
Hi, I’m Krista! I make math courses to keep you from banging your head against the wall. ;)
Math class was always so frustrating for me. I’d go to a class, spend hours on homework, and three days later have an “Ah-ha!” moment about how the problems worked that could have slashed my homework time in half. I’d think, “WHY didn’t my teacher just tell me this in the first place?!”
Converting iterated integrals to polar coordinates (KristaKingMath)
Calculate the iterated integral by converting it to polar coordinates.
Evaluate the iterated integral by converting to polar coordinates - Problem 15.3:42 Cengage Calculus
Convert Double Integrals into Polar Coordinates
How to convert integrals into polar coordinates
Evaluate the iterated integral by converting to polar coordinates - Problem 15.3:39 Cengage Calculus
How to convert integrals into polar coordinates example2
Converting to polar coordinates - double integrals
How to change the order of integration into polar best and easy example (PART-14)
Converting double integrals to polar coordinates (KristaKingMath)
SMN 3033 : Multivariable Calculus - Converting Iterated Integrals to Polar Coordinates -
Evaluate the iterated integral by converting to polar coordinates
How to convert integrals into polar coordinates example1
Iterated Integrals Derive the Polar conversion
Converting Integrals to Polar Coordinates, Superquiz 3 Problem 7
Math 114 - 15.4 - Converting Cartesian Integrals to Polar - The Plug and Chug Series #40
Double Integral (Change to Polar Coordinate)
Calculus 3 Lecture 14.3: Double Integrals over POLAR REGIONS
Sketch the region and convert to polar integration
Evaluate by Changing to Polar Coordinates Double Integral Full Ex
Convert integral to polar example
Double Integral Using Polar Coordinates - Part 1 of 3
Double Integrals
Converting from polar to euclidean double integral becomes much easier!
Комментарии
 0:10:48
0:10:48
 0:07:46
0:07:46
 0:07:39
0:07:39
 0:08:41
0:08:41
 0:12:33
0:12:33
 0:06:27
0:06:27
 0:10:32
0:10:32
 0:05:28
0:05:28
 0:04:43
0:04:43
 0:12:49
0:12:49
 0:20:36
0:20:36
 0:02:18
0:02:18
 0:11:47
0:11:47
 0:07:03
0:07:03
 0:08:08
0:08:08
 0:15:33
0:15:33
 0:09:32
0:09:32
 3:25:15
3:25:15
 0:15:40
0:15:40
 0:07:32
0:07:32
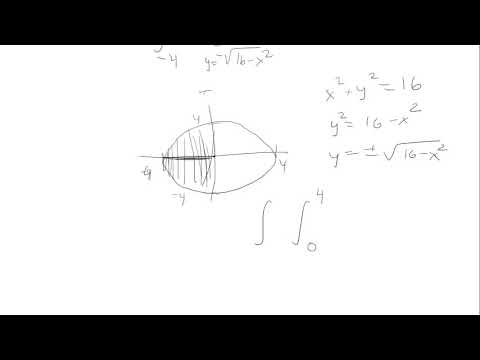 0:02:44
0:02:44
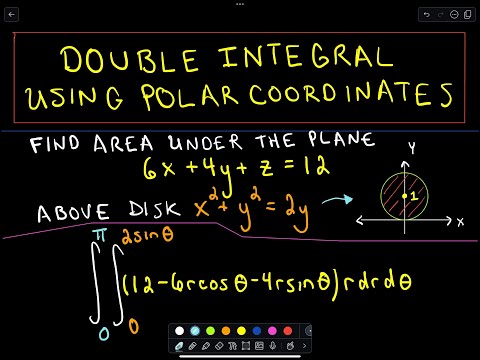 0:05:16
0:05:16
 0:25:02
0:25:02
 0:05:44
0:05:44