Let \( \mathrm{n}_{1}\mathrm{n}_{2}\mathrm{n}_{3}\mathrm{n}_{4}\mathrm{n}_{5} \) be positive int...

preview_player
Показать описание
Let \( \mathrm{n}_{1}\mathrm{n}_{2}\mathrm{n}_{3}\mathrm{n}_{4}\mathrm{n}_{5} \) be positive integers such that \( \mathrm{n}_{1}+\mathrm{n}_{2}+\mathrm{n}_{3}+\mathrm{n}_{4}+\mathrm{n}_{5}=20 \). Then the number of such distinct arrangements \( \left(\mathrm{n}_{1}, \mathrm{n}_{2}, \mathrm{n}_{3}, \mathrm{n}_{4}, \mathrm{n}_{5}\right) \) is
[JEE (Advanced) 2014, 3]
  1. PW Solutions
  2. pw
Рекомендации по теме
Let \( \mathrm{n}_{1}\mathrm{n}_{2}\mathrm{n}_{3}\mathrm{n}_{4}\mathrm{n}_{5} 0:04:44

Let \( \mathrm{n}_{1}\mathrm{n}_{2}\mathrm{n}_{3}\mathrm{n}_{4}\mathrm{n}_{5} \) be positive int...

Let \( \mathrm{n}_{1} 0:10:01

Let \( \mathrm{n}_{1} \) and \( \mathrm{n}_{2} \) be the number of ...

Let \( \mathrm{n}_{1} 0:10:33

Let \( \mathrm{n}_{1} \) and \( \mathrm{n}_{2} \) be the number of ...

Let A={1,2,3,4,5}. Let 0:04:55

Let A={1,2,3,4,5}. Let \(\mathrm{R}\) be a relation on \(\mathrm{A}\) defined by \(x \mathrm{R} ....

Let \( \mathrm{n}_{1} 0:09:06

Let \( \mathrm{n}_{1} \) and \( \mathrm{n}_{2} \) be the number of red and black balls, respecti...

Let \( \mathrm{X}=\{\mathrm{x} 0:04:56

Let \( \mathrm{X}=\{\mathrm{x} \in \mathrm{N}: 1 \leq \mathrm{x} \l...

Let \( S_{n}=\sum_{\mathrm{k}=1}^{4 0:09:20

Let \( S_{n}=\sum_{\mathrm{k}=1}^{4 \mathrm{n}}(-1)^{\frac{\mathrm{...

Let \( \mathrm{A}=\{1,2,3\}, 0:05:26

Let \( \mathrm{A}=\{1,2,3\}, \mathrm{B}=\{2,3,4\} \) and \( \mathrm{C}=\{4,5\} \). Verify that \...

Let \( S=\{1,2,3, 0:09:34

Let \( S=\{1,2,3, \ldots \ldots, 9\} \). For \( k=1,2, \ldots, 5 \), let \( \mathrm{N}_{\mathrm{...

Let \(\mathrm{M}=\left(\frac{-5}{6}\right)^3, \mathrm{~N}=\left(\frac{-2}{3}\right)^2, 0:02:33

Let \(\mathrm{M}=\left(\frac{-5}{6}\right)^3, \mathrm{~N}=\left(\frac{-2}{3}\right)^2, \mathrm{O}...

Let \( f_{\mathrm{n}}(\theta)=\sum_{\mathrm{n}=0}^{\mathrm{n}} 0:10:56

Let \( f_{\mathrm{n}}(\theta)=\sum_{\mathrm{n}=0}^{\mathrm{n}} \fra...

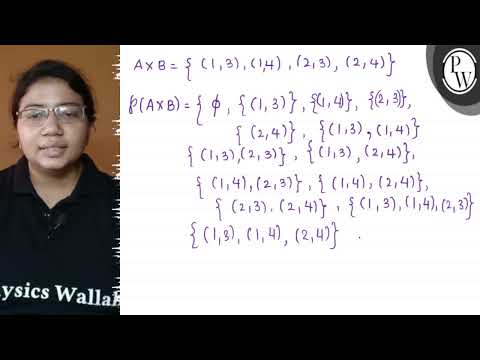
Let \( \mathrm{A}=\{1,2\} 0:06:16

Let \( \mathrm{A}=\{1,2\} \) and \( \mathrm{B}=\{3,4\} \). Write \(...

Let \( \mathrm{a}_{1}, 0:03:10

Let \( \mathrm{a}_{1}, \mathrm{a}_{2}, \ldots, \mathrm{a}_{10} \) b...

Let \( \mathrm{E}=\{1,2,3,4\} 0:04:40

Let \( \mathrm{E}=\{1,2,3,4\} \& \mathrm{~F}=\{1,2\} \). Then the number of onto functions from ...

Let \( \mathrm{n} 0:02:42

Let \( \mathrm{n} \geq 2 \) be an integer. Take \( \mathrm{n} \) distinct points on a circle and...

Let \( \mathrm{n} 0:06:26

Let \( \mathrm{n} \) be the number of ways in which 5 boys and 5 girls can stand in a queue in s...

Let \( \mathrm{f}(\mathrm{x}) 0:02:58

Let \( \mathrm{f}(\mathrm{x}) \) be a differentiable function, sati...

asking minor test 0:00:30

asking minor test marks to allen topper allen kota #allen #allenkota #physicswallah #pw

Let \( D_{\mathrm{r}}=\left|\begin{array}{ccc}2^{\mathrm{r}-1} 0:05:22

Let \( D_{\mathrm{r}}=\left|\begin{array}{ccc}2^{\mathrm{r}-1} & 2....

Let \( x=(2 0:06:21

Let \( x=(2 n+1)(2 n+3) \ldots(4 n-3)(4 n-1) \) and \( y=\left(\frac{1}{2}\right)^{n} \frac{(4 n....

The number of 0:03:19

The number of orbitals with \( \mathrm{n}=5, \mathrm{~m}_{1}=+2 \) is

For any positive 0:05:00

For any positive integer \( \mathrm{n} \), let \( S_{\mathrm{n}}:(0...

Let \( \mathrm{a}_{\mathrm{n}} 0:06:01

Let \( \mathrm{a}_{\mathrm{n}} \) denote the number of all n-digit ...

Let \( \mathrm{w}=\frac{\sqrt{3}+\mathrm{i}}{2} 0:10:00

Let \( \mathrm{w}=\frac{\sqrt{3}+\mathrm{i}}{2} \) and \( \mathrm{P...

Комментарии
Автор

Supper explanation for where you saw the solution sir 😂😂😂

mastermadan