filmov
tv
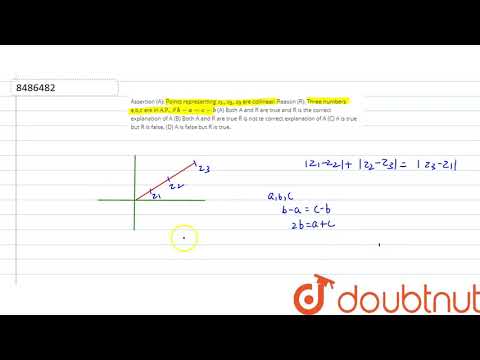
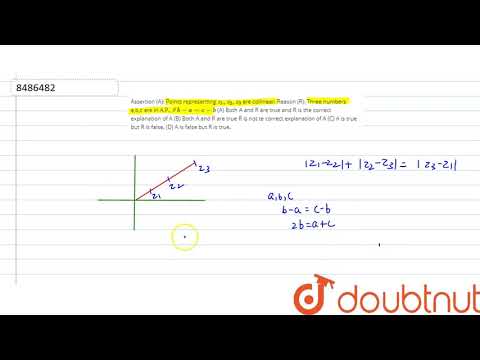
Assertion (A): Three points with position vectors \[ \vec{a}, \vec{b}, \vec{c} \text { are colli...

Показать описание
Assertion (A): Three points with position vectors
\[
\vec{a}, \vec{b}, \vec{c} \text { are collinear if } \vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}=0
\]
Reason (R): Three points \( \mathrm{A}, \mathrm{B}, \mathrm{C} \) are collinear if \( \overrightarrow{\mathrm{AB}}=t \overrightarrow{\mathrm{BC}} \), where \( t \) is scalar.
(A) Both A and R are true and R is the correct explanation of A.br(B) Both A and R are true, but R is not the correct explanation of A.
(C) A is true, but R is false.
(D) A is false, but R is true.
(E) Both A and R are false.
\[
\vec{a}, \vec{b}, \vec{c} \text { are collinear if } \vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}=0
\]
Reason (R): Three points \( \mathrm{A}, \mathrm{B}, \mathrm{C} \) are collinear if \( \overrightarrow{\mathrm{AB}}=t \overrightarrow{\mathrm{BC}} \), where \( t \) is scalar.
(A) Both A and R are true and R is the correct explanation of A.br(B) Both A and R are true, but R is not the correct explanation of A.
(C) A is true, but R is false.
(D) A is false, but R is true.
(E) Both A and R are false.
 0:04:58
0:04:58
 0:03:33
0:03:33
 0:04:08
0:04:08
 0:02:18
0:02:18
 0:04:43
0:04:43
 0:01:22
0:01:22
 0:03:22
0:03:22
 0:03:03
0:03:03
 0:04:27
0:04:27
 0:01:45
0:01:45
 0:22:17
0:22:17
 0:03:22
0:03:22
 0:04:26
0:04:26
 0:04:19
0:04:19
 0:16:25
0:16:25
 0:02:10
0:02:10
 0:00:31
0:00:31
 0:02:19
0:02:19
 0:03:15
0:03:15
 0:02:47
0:02:47
 0:02:06
0:02:06
 0:01:22
0:01:22
 0:06:06
0:06:06
 0:00:14
0:00:14