ESFERA: ÁREA E VOLUME - EP 10 (CURSO COMPLETO)

ESFERA: Geometria Espacial (CURSO COMPLETO)
ESFERA: Definição, Elementos, Seção esférica, Área e Volume
GEOMETRIA ESPACIAL

Volume da esfera
O cálculo do volume de sólidos geométricos é de grande importância para sabermos a capacidade desses sólidos, e com a esfera não é diferente, é de grande importância calcular seu volume para sabermos, por exemplo, a quantidade de gás que podemos colocar em um recipiente esférico, entre outras aplicações. O volume de uma esfera é dado pela fórmula:

Exemplo:

Um reservatório de gás possui um raio igual a 2 metros, sabendo-se disso, qual é o seu volume? (use π = 3,1)

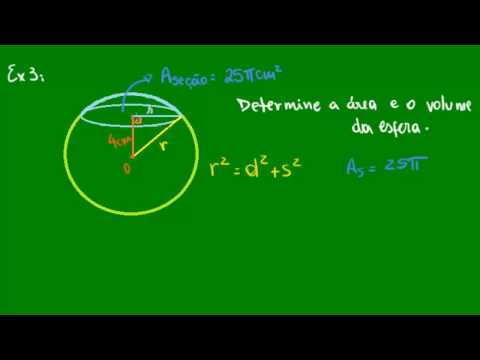
Superfície da esfera
Conhecemos como superfície da esfera a região formada por todos os pontos que estão à distância r da esfera. Note que, neste caso, a distância não pode ser menor, mas sim exatamente igual a r. A superfície da esfera é o contorno de todo o sólido, é a superfície que reveste a esfera. Para calcular a área da superfície da esfera, utilizamos a fórmula:

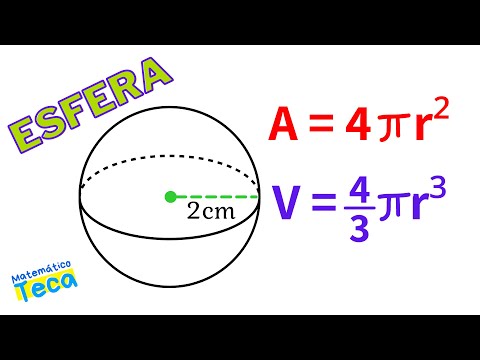
At = 4 π r²
Exemplo:
Em um hospital, será construído um reservatório de gás oxigênio no formato de uma esfera. Sabendo que ele possui 1,5 metro de raio, qual será a área de sua superfície em m²?
At = 4 π r²
At = 4 π 1,5²
At = 4 π 2,25
At = 9 π m²
Partes da esfera
Fuso esférico
Cunha esférica

Qual é a figura esfera?
Conhecemos como esfera todos os pontos no espaço que estão a uma distância igual ou menor que o raio da sua origem, por isso dois elementos importantes dessa figura são o raio r e a origem O. A esfera é classificada como um corpo redondo por conta do formato da sua superfície.

Qual é a figura esfera?
Conhecemos como esfera todos os pontos no espaço que estão a uma distância igual ou menor que o raio da sua origem, por isso dois elementos importantes dessa figura são o raio r e a origem O. A esfera é classificada como um corpo redondo por conta do formato da sua superfície.

Qual é a área de uma esfera?
Dessa forma, é possível definir a área da superfície da esfera como o produto entre 4, o número irracional π e o raio R elevado ao quadrado. O que pode ajudar a memorizar essa fórmula é a sua semelhança com a fórmula da área do círculo, πR2

esfera de revolução, esfera, esferas, área da esfera, volume da esfera, área e volume da esfera, seção esférica, fuso, calota esférica, fuso esférico, cunha esférica, proenem, resolução comentada enem matemática, demonstração do volume da esfera, área da esfera, área da esfera demonstração, volume da esfera demonstração, volume das figuras geométricas, superfície esférica, superfície esférica exercícios resolvidos

[marcelinoboraschi]

Ola
Da um exemplo de calcular volume da tampinha de uma laranja, tendo o raio da laranja