filmov
tv
Oxford Calculus: Jacobians Explained
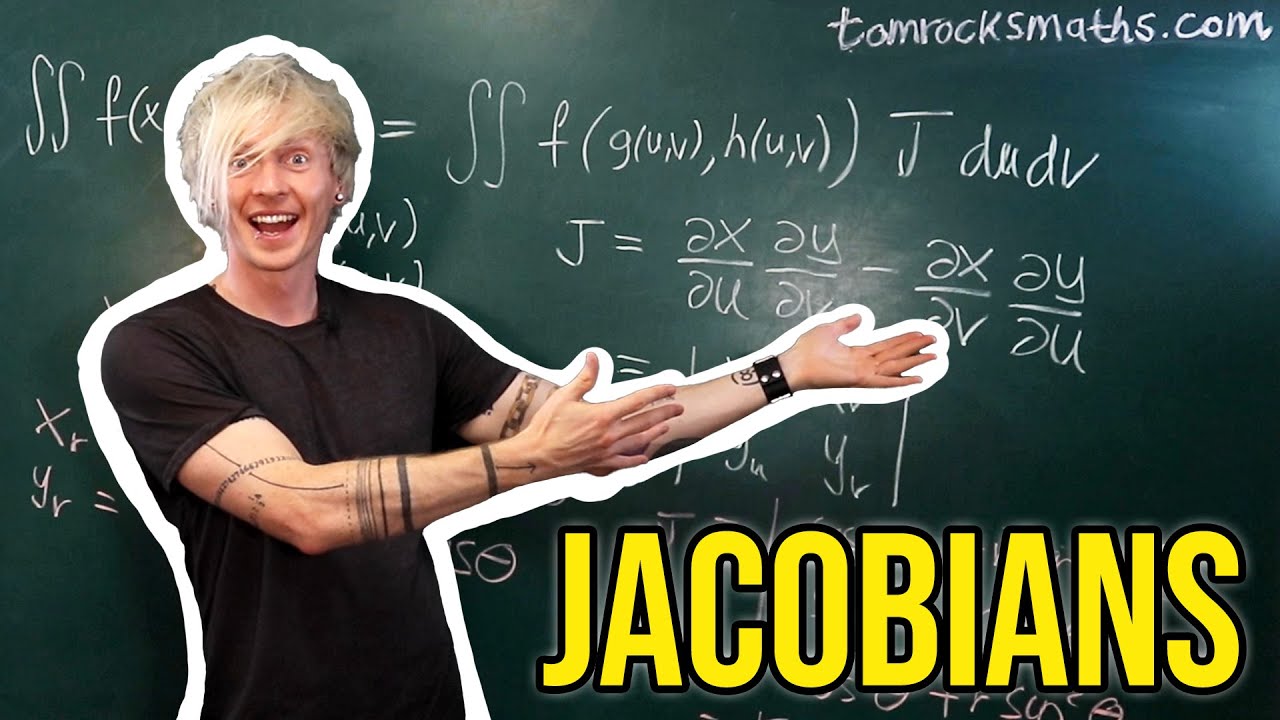
Показать описание
University of Oxford mathematician Dr Tom Crawford explains how to calculate the Jacobian for a 2D coordinate change and applies the general formula to polar coordinates.
We begin with a discussion of when it is appropriate to change coordinates in an integral and how area calculations work in general. This is then exemplified with the unit circle and switching from Cartesian coordinates to polar coordinates where the Jacobian – or ‘stretch factor’ - is given by r.
We then derive the general formula for a 2D Jacobian using a geometrical approach and the deformation of a rectangle to a parallelogram. Finally, the general formula is used to verify the earlier result of the area of the unit circle being equal to pi.
Check your working using the Maple Calculator App – available for free on Google Play and the App Store.
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
We begin with a discussion of when it is appropriate to change coordinates in an integral and how area calculations work in general. This is then exemplified with the unit circle and switching from Cartesian coordinates to polar coordinates where the Jacobian – or ‘stretch factor’ - is given by r.
We then derive the general formula for a 2D Jacobian using a geometrical approach and the deformation of a rectangle to a parallelogram. Finally, the general formula is used to verify the earlier result of the area of the unit circle being equal to pi.
Check your working using the Maple Calculator App – available for free on Google Play and the App Store.
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
Комментарии
 0:29:25
0:29:25
 0:27:14
0:27:14
 0:10:04
0:10:04
 0:07:34
0:07:34
 0:18:22
0:18:22
 0:13:08
0:13:08
 0:19:59
0:19:59
 0:20:44
0:20:44
 0:53:05
0:53:05
 0:27:17
0:27:17
 0:19:14
0:19:14
 0:12:23
0:12:23
 0:00:56
0:00:56
 0:00:12
0:00:12
 0:00:35
0:00:35
 0:48:06
0:48:06
 0:00:16
0:00:16
 0:30:23
0:30:23
 0:10:25
0:10:25
 0:08:58
0:08:58
 0:00:59
0:00:59
 0:00:38
0:00:38
 0:00:50
0:00:50
 0:17:55
0:17:55