filmov
tv
A Stronger Pumping Lemma for Context-Free Languages
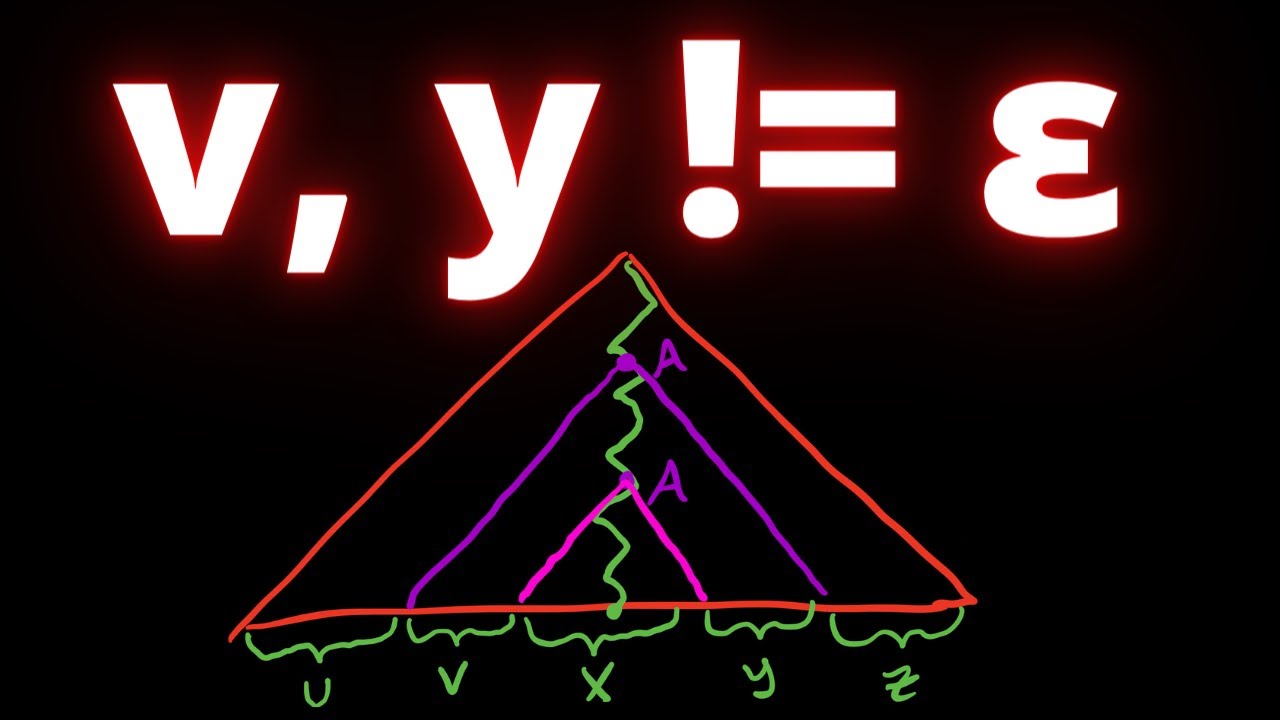
Показать описание
Here we prove a slightly stronger version of the pumping lemma for context-free languages, wherein both the parts that are pumped can be assumed to be non-empty. The trick here is to analyze the parse tree generated in the usual proof, and to make it even taller to avoid the case where one of the parts can be empty.
▶SEND ME THEORY QUESTIONS◀
▶ABOUT ME◀
I am a professor of Computer Science, and am passionate about CS theory. I have taught many courses at several different universities, including several sections of undergraduate and graduate theory-level classes.
▶SEND ME THEORY QUESTIONS◀
▶ABOUT ME◀
I am a professor of Computer Science, and am passionate about CS theory. I have taught many courses at several different universities, including several sections of undergraduate and graduate theory-level classes.
A Stronger Pumping Lemma for Context-Free Languages
Theory of Computation: Pumping Lemma for Regular Languages
Pumping Lemma for Context-Free Languages, Statement and FULL PROOF
Why There's (Likely) No Pumping Lemma for Context-Sensitive Languages
Pumping Lemma for Context-Free Languages: Four Examples
[8a-1] The Pumping Theorem for CFLs - Intuition (COMP2270 2017)
ASU CSE355: Course Review, Examples - Pumping lemma to prove language a^(2n)b^(n+1) not regular
Pumping Lemma for Regular Languages Examples: w#w and ww
Automata Theory - Pumping Lemma for Context-free Languages
Pumping Lemma: Example Problem
Theory of Computation #22: Pumping Lemma (Regular Languages) Overview
Pumping Lemma for Context Free Languages
Pumping Lemma For Context Free Languages (Example)
The p Factorial 'Trick' (Pumping Lemma Technique!)
COMP382 - Theory of Automata - Pumping Lemma for Regular Languages
Pumping Lemma for Context Free Languages - Exercise - Theory of Computing
CONTEXT FREE LANGUAGE WITH PUMPING LEMMA
Sparsification Lemma and ETH
Tutorial 11 - Pumping Lemma for CFL
More Pumping Lemma Examples - CSE355 Intro Theoretical CS 5/30 Pt. 1
Pumping Lemma for Context Free Languages || Lesson 77 || Finite Automata || Learning Monkey ||
The Pumping Lemma for Context-free Languages
Tutorial 6 - FAs and Grammars, The Pumping Lemma
58-Pumping Lemma for Context Free Language
Комментарии
 0:06:39
0:06:39
 0:12:33
0:12:33
 0:30:03
0:30:03
 0:20:15
0:20:15
 0:48:49
0:48:49
![[8a-1] The Pumping](https://i.ytimg.com/vi/Tp_I7vowOU8/hqdefault.jpg) 0:15:45
0:15:45
 0:12:16
0:12:16
 0:09:22
0:09:22
 0:32:06
0:32:06
 0:08:07
0:08:07
 0:09:46
0:09:46
 0:12:53
0:12:53
 0:03:50
0:03:50
 0:11:39
0:11:39
 1:02:11
1:02:11
 0:19:49
0:19:49
 0:01:48
0:01:48
 0:54:48
0:54:48
 1:27:29
1:27:29
 0:48:36
0:48:36
 0:08:44
0:08:44
 0:21:22
0:21:22
 0:57:22
0:57:22
 0:13:47
0:13:47