filmov
tv
Euler's Product for the Zeta function via Boxes II | Math Foundations 241 | N J Wildberger

Показать описание
We continue exploring elementary connections between Box Arithmetic and Number theory, centered on Euler's product formula for the Zeta function. The Fundamental Identity of Arithmetic that we introduced in our last video plays a big role. But now we introduce some interesting variants: when we replace the numbers occurring in this Fundamental Identity with suitable powers of them, including also negative powers, and then apply the Sum operator as before.
What makes this works is a crucial multiplicative property of taking powers.
We make contact with another of Euler's famous formulas, for the sum of the reciprocal squares of natural numbers.
In this talk, we necessarily extend our usual finite careful mathematics with unbounded analogs. But that means that we need to be mindful of the exact meaning of the statements we make. Our general orientation is that the meanings of expression can be reduced to finite expressions by using the natural ordering of the Natural numbers to apply truncation consistently.
Video Contents :
00:00 Introduction
2:42 Powers And The Caret Operation
5:25 Applying f To The FIA
10:45 A Variant ( replacing with cubes)
13:25 Another Variant (replacing with reciprocals)
17:51 Suggests An Identity
19:51 Squared Reciprocals
21:39 Examples
24:32 A calculation
***********************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
What makes this works is a crucial multiplicative property of taking powers.
We make contact with another of Euler's famous formulas, for the sum of the reciprocal squares of natural numbers.
In this talk, we necessarily extend our usual finite careful mathematics with unbounded analogs. But that means that we need to be mindful of the exact meaning of the statements we make. Our general orientation is that the meanings of expression can be reduced to finite expressions by using the natural ordering of the Natural numbers to apply truncation consistently.
Video Contents :
00:00 Introduction
2:42 Powers And The Caret Operation
5:25 Applying f To The FIA
10:45 A Variant ( replacing with cubes)
13:25 Another Variant (replacing with reciprocals)
17:51 Suggests An Identity
19:51 Squared Reciprocals
21:39 Examples
24:32 A calculation
***********************
Here are the Insights into Mathematics Playlists:
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************
Комментарии
 0:07:47
0:07:47
 0:06:05
0:06:05
 0:35:45
0:35:45
 0:58:32
0:58:32
 0:31:22
0:31:22
 0:17:04
0:17:04
 0:15:52
0:15:52
 0:22:11
0:22:11
 0:11:53
0:11:53
 0:13:39
0:13:39
 0:16:26
0:16:26
 0:15:57
0:15:57
 0:05:13
0:05:13
 0:15:11
0:15:11
 0:02:11
0:02:11
 0:00:38
0:00:38
 0:00:49
0:00:49
 0:20:00
0:20:00
 0:00:59
0:00:59
 0:32:32
0:32:32
 0:13:30
0:13:30
 0:05:04
0:05:04
 0:27:59
0:27:59
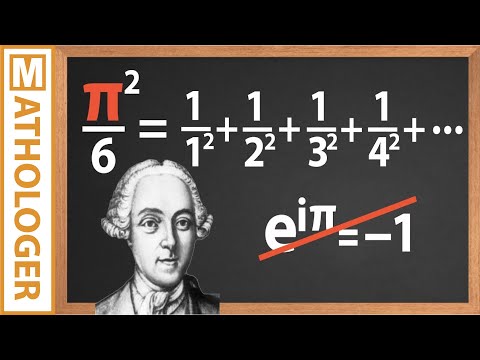 0:17:16
0:17:16