False Position Method In Python | Numerical Methods

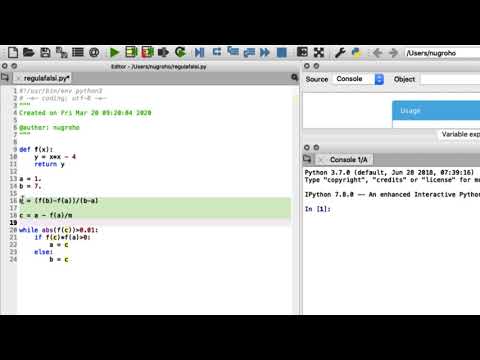
In this video, let’s implement the false position method in Python. The false position method is a non-linear numerical root solver that is commonly taught in numerical methods courses. Through this code we can solve for the roots of any function through the false position method being defined as a function in Python.

This timeline is meant to help you better understand how to perform the false position method in Python:
0:00 Introduction.
0:44 False Position Method In Python.
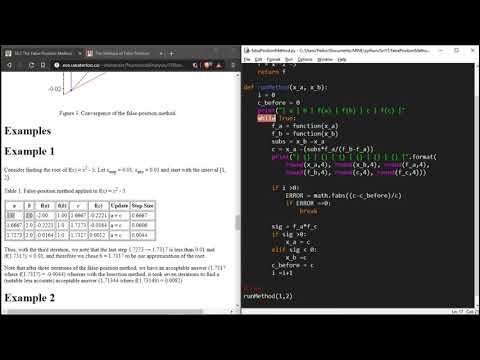
4:40 Solving false position method problems using Python
5:27 Outro

Follow & Support StudySession:

This video is part of our Numerical Methods course. Numerical methods is about solving math problems through approximating the solution of problems that would be difficult or impossible to solve analytically. In this playlist we will cover topics such as solving systems of linear equations, solving systems of non-linear equations, numerical integration, numerical derivatives, etc..
#studysession #numericalmethods #python

[antekkalafior]

Love the video! Very clearly and professionally explained.

[developerx]

The doctor asked me to do it, but based on the estimated error, not the error, and it was resolved successfully. Thank you very much for this wonderful video, sir.😍

[remziogultum]

this video is just next level thank you so much

[samramzi]

def False_Position_Method(func, a, b, error_accept):
"""
This function solves for an unknown root of non-linear funktion given the function, the initial root boundaries,
and an acceptable level of error.

Parameters

func : The user defined function, witch needs to be entered as a string.
a : The inital lower root boundray.
b : The inital upper root boundray.
error_accept : The user's acceptable level of error

Returns

f : The root boundraies and the error at the final iteration.

"""


def f(x):
f=eval(func)
return f

i=0
c_before=0

error=(c-c_before)

while error > error_accept:


if f(a)*f(b)>=0:
print("No root multiple roots present, therefore, the bisection method will not work!")
quit()

elif f(c_after)*f(a)<0:
error=abs(c_after-b)
b=c_after
i= i + 1

elif f(c_after)*f(b)<0:
error=abs(c_after-a)
a=c_after
i=i+1

else:
print("something went wrong")
quit()

print(f"the error remaining is {error}, after {i} iterations")
print(f"the root can be approximately found at {c_after}")
print(f"the lower boundary, a, is {a} and the upper boundray, b, is {b}")




False_Position_Method("(4*x**3)+3*x-3", 0, 1, 0.05)