filmov
tv
Determine The Largest Radical Number? | An Algebra Puzzle
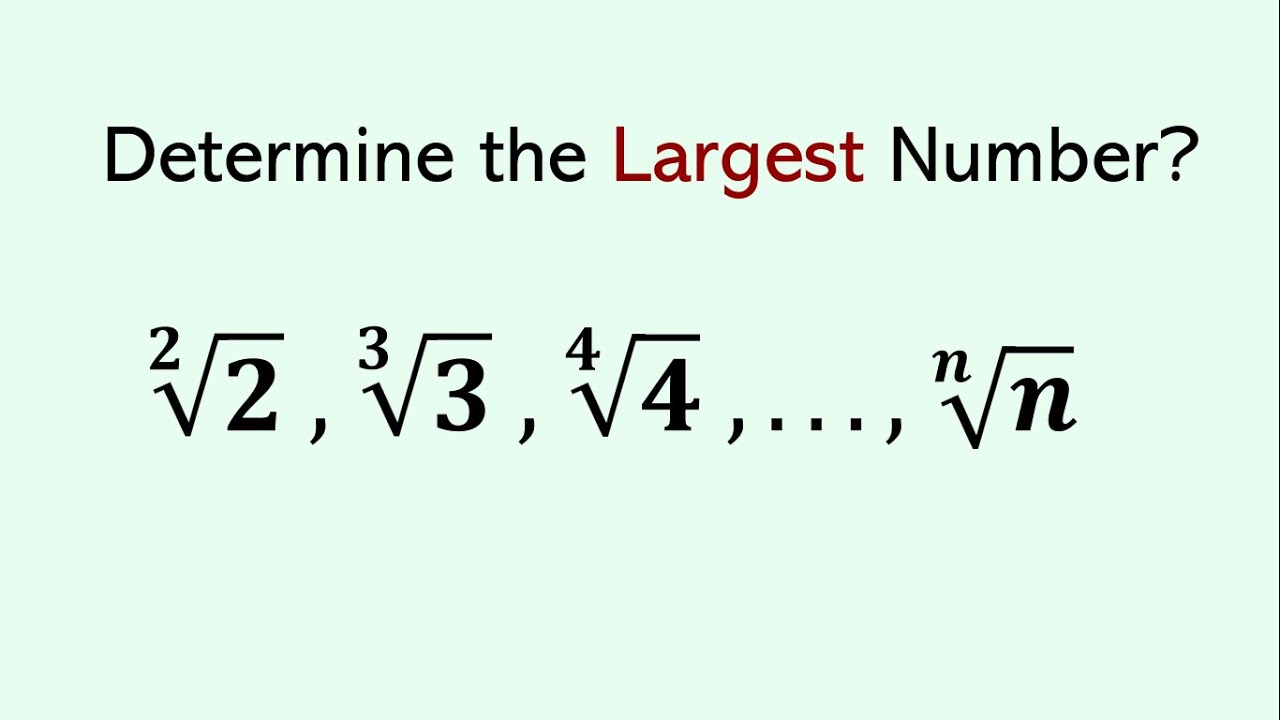
Показать описание
Determine The Largest Radical Number? | An Algebra Puzzle
Ready to solve an intriguing algebra puzzle? In this Math Olympiad challenge, we'll try and understand how to determine the largest radical number in any infinite sequence. This thought-provoking problem will test your algebra skills and push your problem-solving abilities to the next level. Whether you're prepping for a competition or just love solving puzzles, this video is for you! Join me on this mathematical journey and see if you can crack it before I reveal the solution. Don't forget to subscribe for more exciting math challenges!
Topics Shared:
Sequence
Inequalities
Geometric Progression
Algebraic Manipulations
Binomial Expansion
Induction
Math Olympiad
Math Olympiad Preparation
Math Tutorial
#algebra #math #sequence #mathtutorial #matholympiad #largest #radical #numbers
🔍 In this video:
Detailed walkthrough of a challenging algebra problem.
Tips and tricks for solving complex radical sequence.
Encouragement to enhance your problem-solving skills and mathematical thinking.
📣 Call to Action:
Have a go at the problem yourself before watching the solution!
Share your solutions and approaches in the comments below.
If you enjoyed this challenge, give it a thumbs up and subscribe for more intriguing math problems!
🔗 Useful Links:
Don't forget to like, share, and subscribe for more Math Olympiad content!
Thank You for Watching videos !!
Ready to solve an intriguing algebra puzzle? In this Math Olympiad challenge, we'll try and understand how to determine the largest radical number in any infinite sequence. This thought-provoking problem will test your algebra skills and push your problem-solving abilities to the next level. Whether you're prepping for a competition or just love solving puzzles, this video is for you! Join me on this mathematical journey and see if you can crack it before I reveal the solution. Don't forget to subscribe for more exciting math challenges!
Topics Shared:
Sequence
Inequalities
Geometric Progression
Algebraic Manipulations
Binomial Expansion
Induction
Math Olympiad
Math Olympiad Preparation
Math Tutorial
#algebra #math #sequence #mathtutorial #matholympiad #largest #radical #numbers
🔍 In this video:
Detailed walkthrough of a challenging algebra problem.
Tips and tricks for solving complex radical sequence.
Encouragement to enhance your problem-solving skills and mathematical thinking.
📣 Call to Action:
Have a go at the problem yourself before watching the solution!
Share your solutions and approaches in the comments below.
If you enjoyed this challenge, give it a thumbs up and subscribe for more intriguing math problems!
🔗 Useful Links:
Don't forget to like, share, and subscribe for more Math Olympiad content!
Thank You for Watching videos !!
Комментарии
 0:02:20
0:02:20
 0:11:14
0:11:14
 0:02:52
0:02:52
 0:01:32
0:01:32
 0:02:01
0:02:01
 0:02:08
0:02:08
 0:02:27
0:02:27
 0:00:29
0:00:29
 0:02:09
0:02:09
 0:16:55
0:16:55
 0:00:30
0:00:30
 0:43:40
0:43:40
 0:00:39
0:00:39
 0:04:35
0:04:35
 0:00:36
0:00:36
 0:01:11
0:01:11
 0:04:09
0:04:09
 0:01:03
0:01:03
 0:02:36
0:02:36
 0:05:14
0:05:14
 0:03:41
0:03:41
 0:00:53
0:00:53
 0:00:58
0:00:58
 0:08:52
0:08:52