filmov
tv
Newton-Raphson Formula And Derivation | Part 1 of 2

Показать описание
Newton-Raphson’s method is a numerical method for finding the root of a nonlinear equation. This method is for those equations, which are difficult to solve using traditional methods. These equations are also called transcendental equations.
In this video, we will derive the Newton-Raphson’s formula, with the help of graphs and geometry. This will help you understand and visualize the formula and hence make you better at solving the numerical method problems.
For Engineering Mathematics students, GATE aspirants, Diploma students, and math learners - this video is ESSENTIAL for you to have learnt.
Newton-Raphson Method playlist :
In this video, we will derive the Newton-Raphson’s formula, with the help of graphs and geometry. This will help you understand and visualize the formula and hence make you better at solving the numerical method problems.
For Engineering Mathematics students, GATE aspirants, Diploma students, and math learners - this video is ESSENTIAL for you to have learnt.
Newton-Raphson Method playlist :
Newton-Raphson Formula And Derivation | Part 1 of 2
Newton's Method
Newton's method (introduction & example)
Derivation of Newton's Method Formula
How to use the Newton Raphson method
Newton's Method (1 of 2: How does it work?)
Visually Explained: Newton's Method in Optimization
World's Fastest Square Root: Newton's Method
Newton Raphson Method Derivation
The Newton-Raphson Method(NEW!!)| ExamSolutions
Numerical Methods: Derivation of Newton's Method from Taylor Series | A clear, simple explana...
Edexcel A level Maths: 10.3 Newton Raphson Method
||Newton raphson formula||newton raphson method ||newton raphson formula proof||numerical analysis |
Chapter 03.04: Lesson: Graphical Derivation of Newton-Raphson Method
Newton Raphson Method | Numerical Methods | Formula & Example
Explain Newton Raphson Method | Ekeeda.com
A-Level Maths: I2-06 Locating Roots: Introducing the Newton-Raphson Method
Numerical methods 3b - Derivation of Newton Raphson Formula
Newton Raphson method and Secant Method.Derivation
Newton Raphson method || Newtons raphson method in hindi
Advanced calculus & numerical method Newton Raphson method using polynomial equation example(PAR...
NUMERICAL ANALYSIS :KNEC REVISION (NEWTON RAPHSON METHOD)
Newton's Method
Multivariate Newton's Method and Optimization - Math Modelling | Lecture 8
Комментарии
 0:05:41
0:05:41
 0:10:41
0:10:41
 0:20:53
0:20:53
 0:05:23
0:05:23
 0:12:24
0:12:24
 0:13:26
0:13:26
 0:11:26
0:11:26
 0:02:18
0:02:18
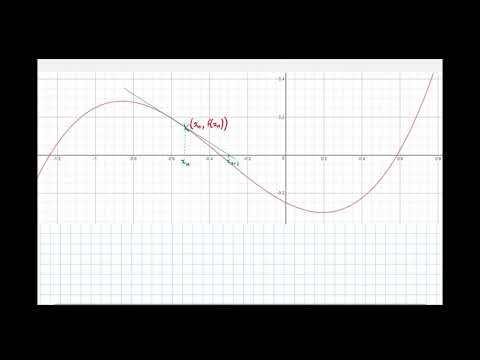 0:06:29
0:06:29
 0:14:59
0:14:59
 0:06:01
0:06:01
 0:06:36
0:06:36
 0:06:32
0:06:32
 0:08:28
0:08:28
 0:21:37
0:21:37
 0:16:25
0:16:25
 0:06:47
0:06:47
 0:09:09
0:09:09
 0:09:41
0:09:41
 0:09:41
0:09:41
 0:06:50
0:06:50
 0:27:50
0:27:50
 0:07:30
0:07:30
 0:26:50
0:26:50