filmov
tv
Mathematical Induction
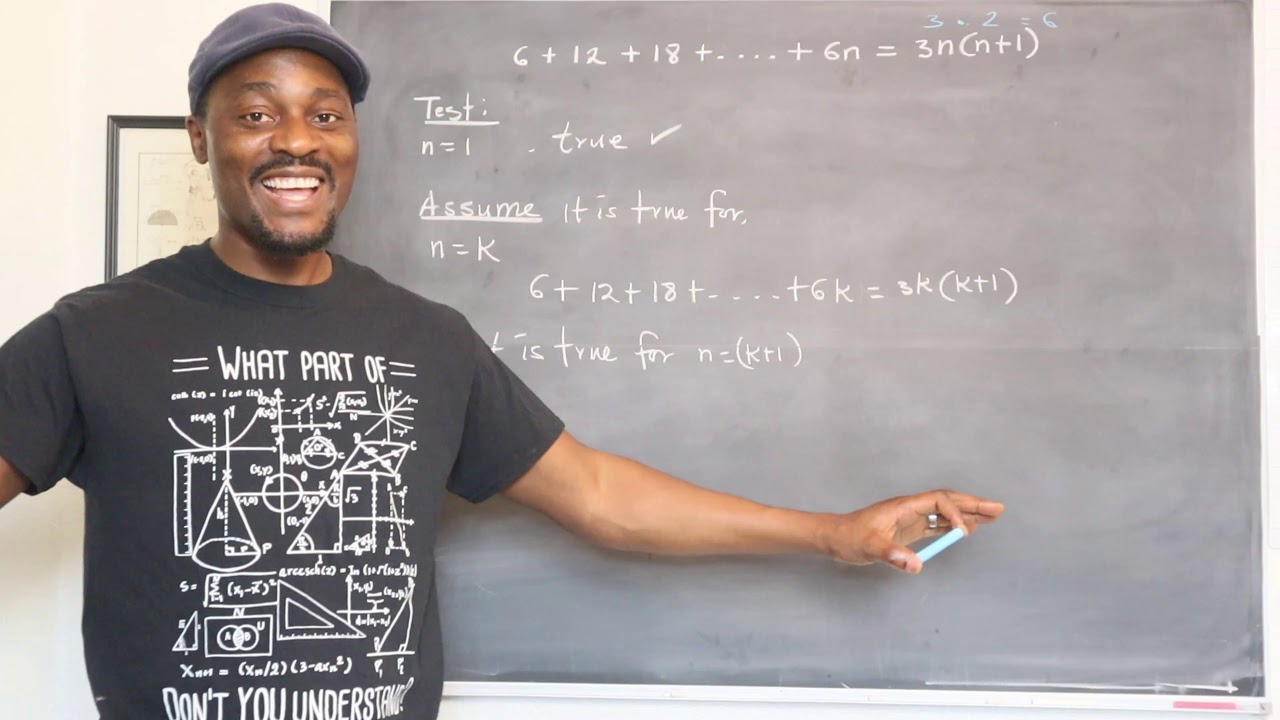
Показать описание
I explained how to prove a formula by induction.
You should try this if you get it.
1+3+5+...+(2n-1) = n^2
You should try this if you get it.
1+3+5+...+(2n-1) = n^2
Mathematical Induction Practice Problems
Proof by Mathematical Induction - How to do a Mathematical Induction Proof ( Example 1 )
Intro to Mathematical Induction
Proof by Mathematical Induction (Precalculus - College Algebra 73)
MATHEMATICAL INDUCTION - DISCRETE MATHEMATICS
Introduction to Mathematical Induction
Proof by induction | Sequences, series and induction | Precalculus | Khan Academy
Principle Of Mathematical Induction | Don't Memorise
5. Exo Suite Récurrence Bac 2023 - Terminale
What does mathematical induction really look like?
Mathematical Induction
Inequality Mathematical Induction Proof: 2^n greater than n^2
Induction Divisibility
Mathematical Induction
Mathematical Induction Examples
Mathematical Induction
Discrete Math II - 5.1.1 Proof by Mathematical Induction
Mathematical Induction 2
Learn how to use mathematical induction to prove a formula
Mathematical induction with inequality
Mathematical Induction - Divisibility Tests (1) | ExamSolutions
Mathematical Induction part1
Mathematical Induction Part 1 Introduction
Proof by Mathematical Induction | Principle of Mathematical Induction | Sample Problems | Part 1
Комментарии
 0:18:08
0:18:08
 0:07:32
0:07:32
 0:12:15
0:12:15
 0:22:35
0:22:35
 0:13:54
0:13:54
 0:20:07
0:20:07
 0:09:23
0:09:23
 0:06:04
0:06:04
 0:00:55
0:00:55
 0:10:51
0:10:51
 0:10:04
0:10:04
 0:09:20
0:09:20
 0:20:35
0:20:35
 0:13:53
0:13:53
 0:12:14
0:12:14
 0:13:06
0:13:06
 0:13:01
0:13:01
 0:35:39
0:35:39
 0:07:08
0:07:08
 0:12:53
0:12:53
 0:08:35
0:08:35
 0:20:34
0:20:34
 0:11:08
0:11:08
 0:13:24
0:13:24