filmov
tv
Counting non-Negative Integer Solutions to x + y + z = 21 with Constraints

Показать описание
Anybody who knows how to count numbers of possible distributions of IDENTICAL objects (such as candies or apples) between DISTINCT recipients (such as people or numbered boxes) also knows how to count the number of non-negative integer solutions to equations such as x + y + z = 21, even though they may not realise it.
After watching this video, answering the two types of questions will hopefully be equally simple, which is good news because these types of questions are a mainstay of Maths Olympiads and College Entrance Exams.
For more videos on identical/distinct counting see our playlist 'Counting Identical/Distinct Distributions'
For more videos on counting see our playlist 'Counting'
For more videos on diophantine equations, see our playlist 'Diophantine Equations'
For more videos on permutations and combinations, see our playlist 'Perms and Combs'
For more videos on Maths Olympiads see our playlist 'Maths Olympiads'
For more JEE Aspirant videos see our playlist 'JEE Aspirants'
For more videos on College Entrance Exams, see our playlist 'UPCAT and other CETS'
After watching this video, answering the two types of questions will hopefully be equally simple, which is good news because these types of questions are a mainstay of Maths Olympiads and College Entrance Exams.
For more videos on identical/distinct counting see our playlist 'Counting Identical/Distinct Distributions'
For more videos on counting see our playlist 'Counting'
For more videos on diophantine equations, see our playlist 'Diophantine Equations'
For more videos on permutations and combinations, see our playlist 'Perms and Combs'
For more videos on Maths Olympiads see our playlist 'Maths Olympiads'
For more JEE Aspirant videos see our playlist 'JEE Aspirants'
For more videos on College Entrance Exams, see our playlist 'UPCAT and other CETS'
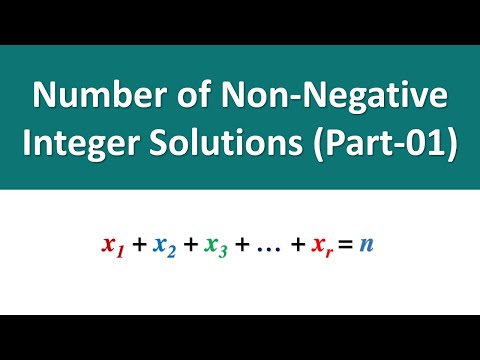 0:06:01
0:06:01
 0:03:24
0:03:24
 0:08:24
0:08:24
 0:09:41
0:09:41
 0:04:46
0:04:46
 0:01:23
0:01:23
 0:02:01
0:02:01
 0:01:00
0:01:00
 0:06:46
0:06:46
 0:03:27
0:03:27
 0:04:31
0:04:31
 0:08:52
0:08:52
 0:23:16
0:23:16
 0:03:32
0:03:32
 0:03:37
0:03:37
 0:07:22
0:07:22
 0:05:26
0:05:26
 0:02:42
0:02:42
 0:10:53
0:10:53
 1:11:20
1:11:20
 0:12:40
0:12:40
 0:08:06
0:08:06
 0:04:20
0:04:20
 0:29:25
0:29:25