Exponential scale vs Linear scale

The calculation for linear is:

Bf+(Bf/x)*y

Whereas for exponential it's:

Bf*2^(y/x)

Where Bf is the Base frequency, x is the tone system, y is the interval.

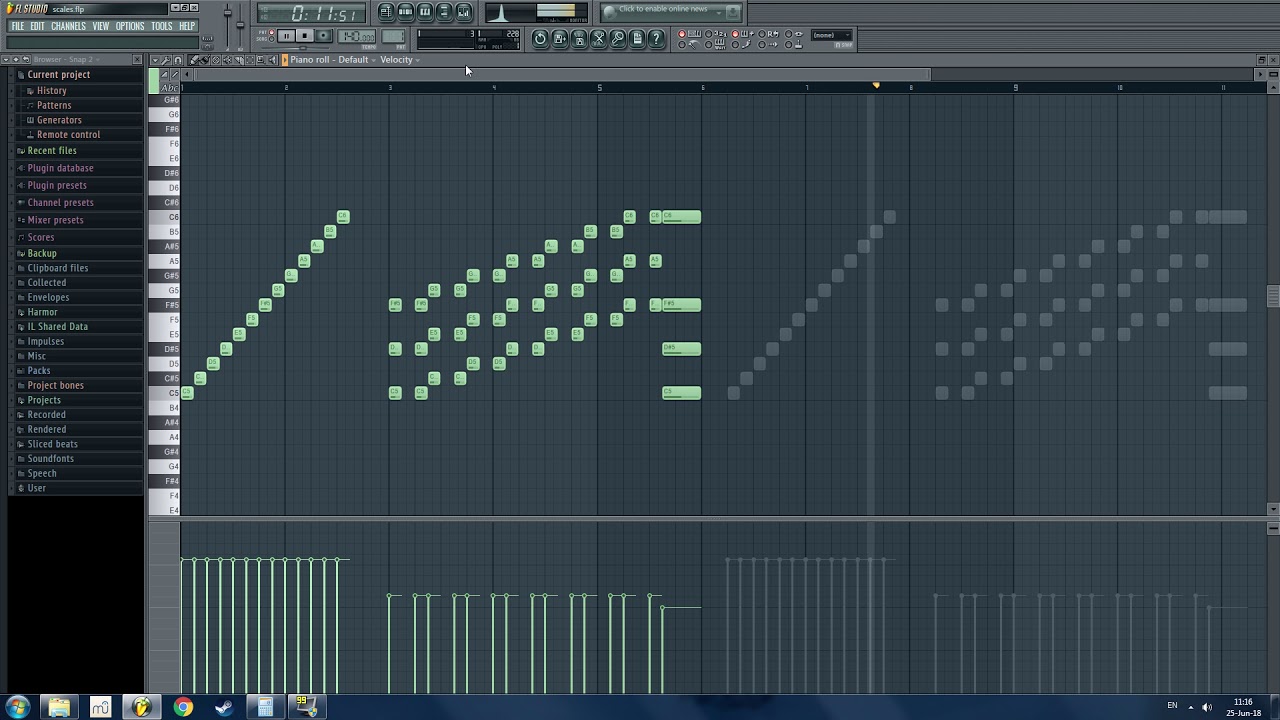
You can see their relationship very clearly when you plot both of them. If we assume a base frequency of 200Hz, and a 12-tone system:
Linear:
200.000 = C
216.667 = C# (sharp)
233.333 = D# (flat)
250.000 = E (perfect)
266.667 = F (perfect)
283.333 = F# (sharp)
300.000 = G (perfect)
316.667 = G# (flat)
333.333 = A (perfect)
350.000 = A# (perfect)
366.667 = A# (sharp)
383.333 = B (sharp)
400.000 = C

Exponential:
200.000 = C
211.893 = C#
224.492 = D
237.841 = D#
251.984 = E
266.968 = F
282.843 = F#
299.661 = G
317.480 = G#
336.359 = A
356.359 = A#
377.550 = B
400.000 = C

The linear system is basically an extension of the harmonic series, which has the calculation:

Bf+Bf*y

Because of this, arguably all tones in any linear scale are tuned perfectly, but they might not be in our standard tuning system. A linear scale with 12 tones is the equivalent of starting at the 12th harmonic, or the fifth 3 octaves above the root.
In fact, the number of tones you pick for your system is the place at which the harmonic series uses the same tuning.

[iainburge]

Stumbled onto this after you replied to one of my comments. Neat stuff, what exactly do you mean by perfect in the description? Justly tuned?