filmov
tv
Красивый ребус олимпиады седьмого класса. #математика #ребус #олимпиада #7класс #simplemath #изи

Показать описание
Красивый ребус олимпиады седьмого класса. #математика #ребус #олимпиада #7класс #simplemath #изи...
Классная задача на логику из олимпиады 7 класса
Ребус для крепких орешков. #математика #ребус #головоломка #пазл #арифметика...
Олимпиада 7 класса за минуту. Люди и грибы, единственное решение. #математика #арифметика #счет...
Ребус для 5 класса. Слабо решить? Многие взрослые впадают в ступор...
Олимпиада для 7 класса
Попробуй решить математический ребус
Трехэтажная степень
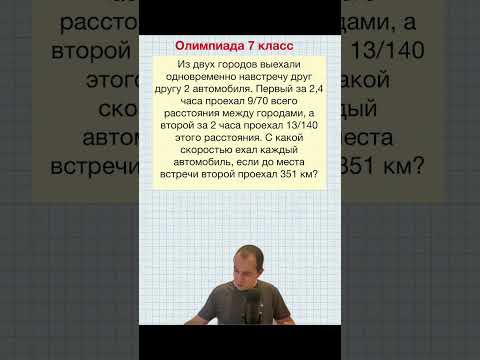
Как думать решая олимпиадки. Задача на движение 7 класс. #олимпиада #математика #алгебра #движение...
Как решить ребус?
Детский ребус: ПЧЁЛКА•7=ЖЖЖЖЖЖ
Задание из 7 класса! #shorts
Как умножать сложные числа? Лайфхак👌 #shorts
Хитрая задача на логику и сообразительность, которую решит не каждый...
Я В ШОКЕ😳Лайфхак, как умножать на пальцах 😎 Таблица умножения легко...
на олимпиаде по математике😠 #meme #мемы #олимпиада #школа...
ДТП - кто виноват?) #АзбукАСпорта #волейбол #дети #ярцево...
8 ЛОГИЧЕСКИХ ЗАГАДОК ДЛЯ САМЫХ УМНЫХ! Насколько хорошо развит твой мозг?...
Мои начинания в ОЛИМПИАДАХ и КОНКУРСАХ #учеба #study #олимпиада #конкурс #7класс...
Олимпиада для 5-7 классов! регистрируйтесь и участвуйте! #всош #олимпиады #олмат...
Ребус с двумя решениями не для слабаков
математические ребусы! #shorts
За кого вы болели?🥺 #олимпиада #александратрусова
Хитрая задача про монету #задача #математика #репетитор #олимпиада...
Комментарии
 0:01:00
0:01:00
 0:02:01
0:02:01
 0:00:48
0:00:48
 0:00:52
0:00:52
 0:04:34
0:04:34
 0:00:58
0:00:58
 0:00:11
0:00:11
 0:00:57
0:00:57
 0:00:46
0:00:46
 0:01:34
0:01:34
 0:05:51
0:05:51
 0:00:59
0:00:59
 0:00:59
0:00:59
 0:03:00
0:03:00
 0:00:28
0:00:28
 0:00:08
0:00:08
 0:00:22
0:00:22
 0:07:59
0:07:59
 0:01:00
0:01:00
 0:00:39
0:00:39
 0:06:07
0:06:07
 0:00:27
0:00:27
 0:00:11
0:00:11
 0:01:00
0:01:00