Lissajous Figures Explained | SHM | A question from JEE Main 2018 | JEE Physics | IIT JEE

Lissajous figure, also called Bowditch Curve, pattern produced by the intersection of two sinusoidal curves the axes of which are at right angles to each other
In JEE Main 2018 a question was asked on Lissajous Figures in Physics. It is a concept of Superposition of SHM.

Question
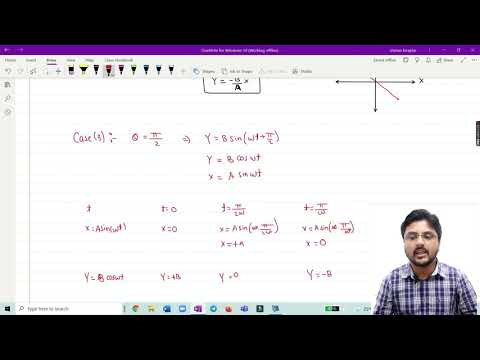
Two simple harmonic motions, as shown below, are at right angles. They are combined to form Lissajous figures. x(t) =A sin (at+δ) y(t) =B sin (bt) Identify the correct match below. Parameters Curve

#LissajousFigures #PhDSeries #Eduniti #JEEMain #IITJEE #JEEAdvanced #JEE2022 #JEE2023 #JEEMain2022 #SHM
#Physics #IITJEEPhysics #Class11

[mohitgoenka]

In JEE Main 2018 a question was asked on this concept. Watch the full video to get complete grasp on this topic.

[vivychauhan]

Never heard about this topic, fortunate to have you, who even cares for a single question from a topic students are unfamiliar with. Thanks for being yourself sir, Never change!!🙏🙏👑👑

[hardikjain]

We want teacher like him for maths and chemistry too ❤❤

Huge respect for this guy🌠

[joshhr]

Concept :
Eliminate time(t) from the given two equations and, form an equation in x and y to get the final curve/path of SHM.

[amcreationmusic]

this question is discuss in my classs but I didn't get it, now I'm fully understand this small topic❣️🙏🏻thank u sir

[zaidshaikh]

THIS IS A QUESTION WHICH I LEFT WHEN I DONE WITH SHM NOW THIS CONCEPT IS ALSO CLEAR LOVE YOU MOHIT SIR👍

[iitjeeaspirant]

He is One of the greatest because he does not skip any single topic

[shivpratapsinghspsingh]

Sir I was watching your guidance videos since last few days, I thought you are just a normal educator but today for the first time I watched your teaching session of Lissajous figures and saw your tricks playlist and realized that what I was thinking a Nano is actually a Rolls Royce,
Your new fan sir❤
Charan sparsh Sir🙏

[riyasingh]

Thank you
Wo kehte h na "ek teer s 2 nishane"
But sir has made it "ek teer s jitne bhi h saare nishane"😎🤗

[subhashreepanda]

It's a new concept to me. I can't do this question while practicing pyqs . But a big thanks to you sir for discussing this problem. Thank you so much. 🙏🙏

[enddistraction]

That Was easy question. I solved it correctly, but the term "LISSAJOUS FIGURE" was new to me. Good to know about it :->

[ananyaxbhardwaj]

Didn't know about this concept, Thankyou bhaiya .. ☀️
Also a request to bring an advice video for JEE 2023 . Soon we ll starting our 12th so the requirements and other useful things wil really really help
THANKYOU BHAIYA.😃 YOU ARE AN INSPIRATION 🌟 I ABSOLUTELY LOVE THIS CHANNEL

[ankitroy]

sir in this question we can find the answer via parametric form....x/A=sin at, and y/B=cos bt hoga toh circle, A=/=B toh ellipse

[TawhidCodex]

Just abhi 1st shift of 28 June dekar aaya hun

Jab is concept se question aaya toh maza aa gaya tha dekhkar

[NishantHegde]

Thanks! This is the best video on Lissagous Figures that I could have ever found on youtube.

[himanshu_yadav_]

Concept- eliminate time from both equations using simple trigonometry .

[parthsarathidixit]

Heard this topic for 1st time
Next phd Topic suggestion : Dielectric in capacitors with variable cases and energy changes while insertion.

[sujeetgund]

Me vibing in alone who already did some class illustrations like this type of questions!

[AniranPaul]

Thank you sir, Did not study about this topic in my JEE days, but have come back to your channel to study this topic in my BTECH days. Love from Jadavpur University🥰❤

[chiragjain]

thank you sir i read shm about 5-6 months ago.
and now just seeing your revision video twice i can grab all the topics to the point
thank you sir for all your content on you tube. :)