filmov
tv
Solving 2002 Sweden Math Olympiad Question | Solving a Symmetrical System of Equations

Показать описание
🔴Solving 2002 Sweden Math Olympiad Question | Solving an if then question using a Symmetrical System of Equations
Hello there.
In this video, we are dealing with one of the 2002 Sweden math olympiad questions, where we are given a nice symmetrical system of equations, and we are supposed to evaluate an expression.
🔴I hope you enjoy watching this video.🔴
Don't forget to:
✅ Leave a comment
✅ Subscribe
✅ Hit the like button
✅ Ring the bell
topics covered in this video:
system of equations
system of equations from sweden
math olympiad question
how to evaluate
if then question
#MathOlympiadQuestion #SystemOfEquations #AnonMath
Solving 2002 Sweden Math Olympiad Question | Solving a Symmetrical System of Equations
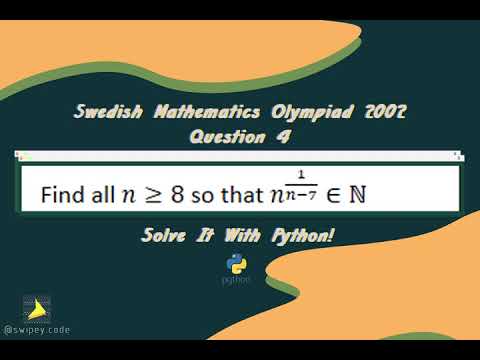
Swedish Mathematics Olympiad | 2002 Question 4
Swedish Mathematics Olympiad 2002 Question 4 | Solve It With Python! (Bahasa Indonesia)
amazing equation of Sweden math Olympiad
croatian Mathematical Olympiad 2002
croatian Mathematical Olympiad 2002
Olympiad Mathematics - A Nice Algebra Problem | Sweden Junior Math Olympiad
Indian Math Olympiad 2002 Q3 | Can you solve the inequality?
Olympiad Mathematics | Algebra | Math Problems | Sweden Junior Math Olympiad
Sweden Math Olympiad problem | Algebra Challenge
Math Olympiad Question | Solving a System of Equations with Logarithm in 2 Ways
Can you solve this grade 10 Swedish national math problem?
AMERICAN MATH OLYMPIAD-1989:Solve The System Of Equations!
Canadian Math Olympiad 2022-Learn How To Solve It!
amazing equation of Germany math olympiad
Olympiad Math | Solve for x | How? | RMD
Nice Math Olympiad Question
Math Olympiad Question | Equation Solving | You should use this trick
Math Olympiad Problem | Solving a Nice Radical Equation Involving Exponents with 2 Methods
Canadian Mathematical Olympiad Problem
Math Olympiad Question 🚩
Solving a System of Equations from Iran | Solving the 2005 Iranian Math Olympiad Question
A problem possibly(?) from HMMT 2002 (Harvard MIT mathematics tournament)
Solving a Nice Functional Equation from Math Olympiad
Комментарии
 0:07:40
0:07:40
 0:14:19
0:14:19
 0:18:18
0:18:18
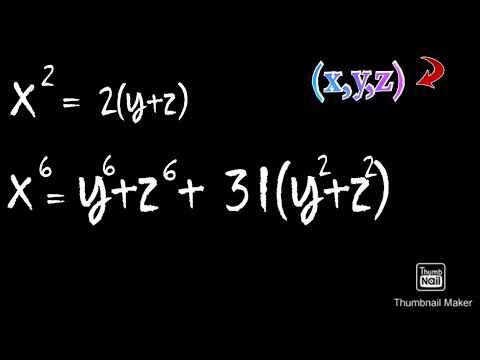 0:07:42
0:07:42
 0:11:27
0:11:27
 0:06:49
0:06:49
 0:02:37
0:02:37
 0:04:56
0:04:56
 0:02:36
0:02:36
 0:07:39
0:07:39
 0:09:50
0:09:50
 0:03:33
0:03:33
 0:07:30
0:07:30
 0:08:41
0:08:41
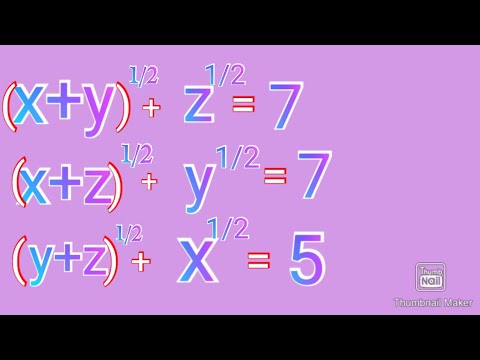 0:17:59
0:17:59
 0:06:22
0:06:22
 0:04:09
0:04:09
 0:05:10
0:05:10
 0:11:16
0:11:16
 0:06:42
0:06:42
 0:04:12
0:04:12
 0:07:39
0:07:39
 0:03:18
0:03:18
 0:10:48
0:10:48