filmov
tv
¿Puedes calcular el valor de x? | ARTIFICIOS ALGEBRAICOS

Показать описание
En el presente vídeo se resuelve una ecuación exponencial (nivel avanzado) por artificios algebraicos.
Calcular x, 4^x + 6^x = 2(9^x)
#AcademiaInternet, #algebradesdecero
Calcular x, 4^x + 6^x = 2(9^x)
#AcademiaInternet, #algebradesdecero
¿Puedes calcular el valor de x? | (DEMOSTRACIÓN DE LA FÓRMULA)
¿Puedes calcular el valor de x? |
¿Cómo puedo calcular el valor del kilowatt/hora que estoy pagando?
¿Puedes calcular el valor de x? | ARTIFICIOS ALGEBRAICOS
¿Puedes calcular el valor de A + B en la siguiente igualdad? | [FRACCIONES PARCIALES]
Puedes calcular x en menos de 1 minuto
¿Puedes calcular el valor de x usando artificios algebraicos? | [raices infinitas]
¿Puedes calcular el valor de x en la siguiente figura?
Calcular arriendo en Colombia con Nuevo IPC
¿Puedes calcular el valor de x en x^x^x^x^x³=3? | [ARTIFICIOS ALGEBRAICOS]
¿Puedes calcular el valor del angulo x°? | Nivel bachillerato
¿Puedes calcular el valor de x utilizando TRAZOS AUXILIARES en triangulos | NIVEL AVANZADO
TRUCO MATEMÁTICO PARA CALCULAR PORCENTAJES
¿Puedes calcular el valor de x? | [La respuesta NO es 4]
¿Puedes calcular el valor de un arco de circunferencia? | GEOMETRIA
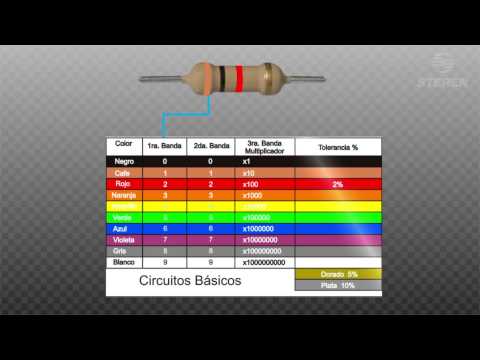
Cómo calcular el valor de una resistencia con el Código de Colores
¿Puedes calcular el valor del angulo x? | [Angulos en la circunferencia] |
¿Vendes productos? Te enseño a calcular el precio correcto al que los debes vender ☝🏼
Puedes calcular el lado del triangulo equilátero ABC
¿Puedes calcular el valor del angulo x en la figura? | [Angulos en la circunferencia] |
¿Puedes calcular la altura del farol en el siguiente reto geometrico? | ¿Falta información?
#Shorts| Puedes calcular z en menos de 1 minuto
¿Puedes calcular esta Integral definida rápidamente? #maths #quiz #calculus
Como calcular el PORCENTAJE DE UNA CANTIDAD CON RESPECTO AL TOTAL %
Комментарии
 0:06:51
0:06:51
 0:06:57
0:06:57
 0:00:31
0:00:31
 0:08:12
0:08:12
 0:08:01
0:08:01
 0:00:54
0:00:54
 0:05:12
0:05:12
 0:07:12
0:07:12
 0:00:51
0:00:51
 0:06:24
0:06:24
 0:04:11
0:04:11
 0:07:36
0:07:36
 0:00:50
0:00:50
 0:11:00
0:11:00
 0:06:12
0:06:12
 0:03:24
0:03:24
 0:06:46
0:06:46
 0:01:01
0:01:01
 0:07:07
0:07:07
 0:06:21
0:06:21
 0:05:11
0:05:11
 0:00:59
0:00:59
 0:00:46
0:00:46
 0:02:44
0:02:44