Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (2 of 92) Normalization of the Wave Equation

preview_player
Показать описание

In this video I will explain the normalizing the wave equation of Schrodinger equation and the probability of finding the particle in a particular position.

Next video in this series can be seen at:
  1. Michel van Biezen
  2. ilectureonline
  3. ilectureonline.com
  4. Mike
  5. Mike van Biezen
  6. van Biezen
Рекомендации по теме
Physics - Ch 0:07:41

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (1 of 92) The Wave Equation

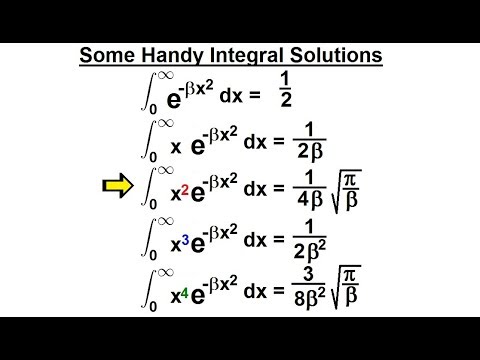
Physics - Ch 0:01:38

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (59 of 92) Some Handy Integral Solutions

Physics - Ch 0:02:40

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (69 of 92) Is this Possible???

Physics - Ch 0:02:56

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (54 of 92) The wave Function

Physics - Ch 0:07:03

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (2 of 38) How are Photons Absorbed? 1

Physics - Ch 0:03:38

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (49 of 92) How Oscillators Increase Energy

Physics - Ch 0:01:53

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (17 of 38) E=mc^2 and the Mass of Proton

Physics - Ch 0:03:24

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

Light (lec -4) 0:55:05

Light (lec -4) | class 10 | physics ch-1 (Raw lecture) | NODOUBT CLASSES JBP

Physics - Ch 0:06:55

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (4 of 38) Absorber Thickness

Physics - Ch 0:04:59

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (42 of 92) k=? of a Diatomic Molecule

Physics - Ch 0:03:48

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (40 of 92) What is Reduced Mass?

Physics - Ch 0:05:50

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (80 of 92) Transmission Coeff. Example

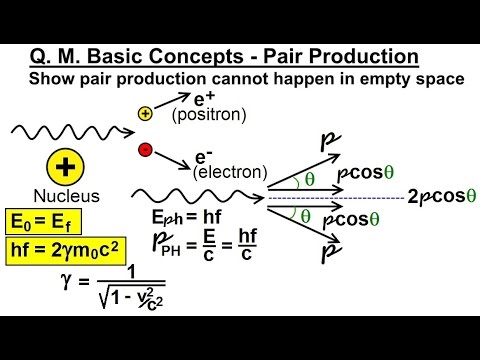
Physics - Ch 0:07:19

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (1 of 38) What is Pair Production?

Physics - Ch 0:05:40

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (92 of 92) Modeling Polonium-212 Decay

Physics - Ch 0:05:50

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (32 of 92) Finite Potential Well Part 1

Physics - Ch 0:06:22

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (5 of 38) Absorber Thickness: Example

Physics - Ch 0:09:45

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (14 of 38) What is Gravitation Redshift? 1

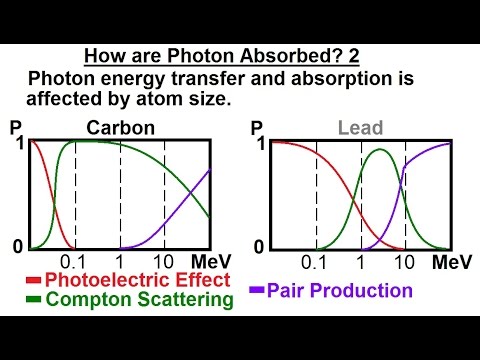
Physics - Ch 0:04:34

Physics - Ch 66 Quantum Mechanics 2: Basic Concepts (3 of 38) How are Photons Absorbed? 2

Physics - Ch 0:04:10

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (81 of 92) Transmission Coeff., Original Eq

Physics - Ch 0:08:23

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (67 of 92) Finding R=? T=? Coefficients

Physics - Ch 0:07:07

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (13 of 92) Time & Position Dependencies ...

Physics - Ch 0:07:05

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (91 of 92) Modeling Polonium-212 Decay

Physics - Ch 0:03:02

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (53 of 92) The wave Equation

Комментарии
Автор

If I pass my quantum mechanics final next week it's all thanks to you, sir. You're getting me through my physics degree, thank you.

valemessi
Автор

wow he's awesome!! i hope we had prof like u in my IIT

SurajKumar-zkem
Автор

You were literally my saving grace by putting those videos about quantum physics.
1 week ago I started my 2nd year (physics degree) and we started learning quantum physics, and after the first day i went home with a major headache, my professor wasn't clear with the subject and I was very confused, and on top of that he bombarded us with lots of homework...
On the way back home I prayed hard that when I go to your channel and type "quantum mechanics" in the search box it will show something.
Thank you so much for covering this topic, very few people can present this topic at our level of understanding (the students).


Your'e an incredible person, thank you so much for all the effort your'e putting into this.

stivraptor
Автор

Thank you very much, such a great explanation .

DiegoAToala
Автор

Are electrons actual particles or an excitation in an electron field?

sandlertossone
Автор

I'm not sure about something : the probability density of the wave function is for all space, and the probability of finding a particle is for a particular place of the space, that's the difference between the two?

guilhemescudero
Автор

I used to watch your videos for AP Physics 1, then AP Physics C, Calculus, and now Quantum Mech. You are truly something else.

John-lfxf
Автор

why will the number we end up be greater than one ??

markdonald
Автор

I'm from Nigeria and this really helped

master-ikro
Автор

He is fantastic. Why must the wave function be continuous and why must its derivative be continuous.. what is the conservation law that demands this?

paulg