0.7 An Uncountable Set

Describing a set with cardinality greater than that of the natural numbers and proving this fact about it

Some things to think about:

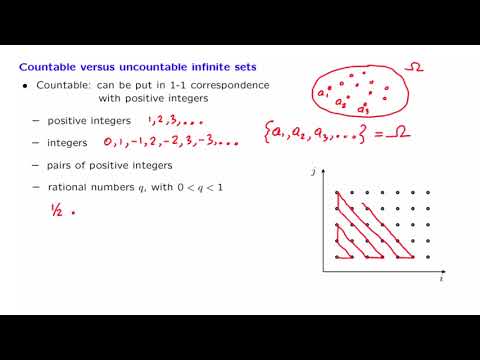
Here we used a list of elements to construct an element that wasn't on the list by making sure it was different from each element on the list. This process is called diagonalization.

With this proof and what we did last time, we can show that there are more numbers on the real line, of even on the interval (0,1) than can be expressed using finite sequences of symbols. In fact this difference in cardinality means that if we were to pick a number at random on the real line, there is probability 1 that it cannot be expressed using finitely many symbols.