filmov
tv
Introduction to Proofs 1.1 Pythagorean Triples. Showing that at least one number is even.

Показать описание
In this video, we are going to use some of the proof techniques to show that at least one number from Pythagorean Triple must be even.
-~-~~-~~~-~~-~-
Please watch: "Real Projective Space, n=1"
-~-~~-~~~-~~-~-
-~-~~-~~~-~~-~-
Please watch: "Real Projective Space, n=1"
-~-~~-~~~-~~-~-
Introduction to Proofs 1.1 Pythagorean Triples. Showing that at least one number is even.
1.1.2 Intro to Proofs: Part 1
Only U.S. President to prove a theorem
Pythagorean Theorem: Six Proofs
#1 Pythagorean Theorem Proof: Simple Proof
Pythagorean Theorem - A simple Introduction and Proofs
An Introduction to the Pythagorean Theorem | Math with Mr. J
Proof #1 of the pythagorean theorem
Episode 1: Proof of the Pythagorean Theorem [#MathChops]
Simple Pythagorean Dissection Proof
ENGT 509 Intro 1-2 Pythagorean Theorem
Gougu ('Pythagorean') Theorem - Part 1
3 Fine Proofs of the Pythagorean Theorem
Pythagorean Theorem
Pythagorean Theorem Proof 1st out of 7 proofs (Visual Proof) - 1 minute long
New Pythagorean Theorem Proof: From Two New Orleans High Schoolers!
Math Antics - The Pythagorean Theorem
Proofs #1 (introduction and ex. 1)
Pythagorean Theorem II (visual proof)
G1 TOPIC 7-1 Pythagorean Theorem (12.26min)
Proving the Pythagorean Theorem
USL: Pythagorean Theorem Proofs - Introduction & Prerequisites
All possible pythagorean triples, visualized
Visual Proof of the Pythagorean Theorem | 1
Комментарии
 0:09:30
0:09:30
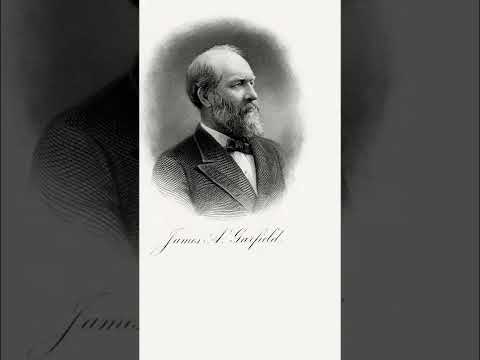 0:01:00
0:01:00
 0:01:00
0:01:00
 0:19:17
0:19:17
 0:10:25
0:10:25
 0:12:55
0:12:55
 0:00:48
0:00:48
 0:03:53
0:03:53
 0:00:59
0:00:59
 0:03:00
0:03:00
 0:04:44
0:04:44
 0:15:36
0:15:36
 0:11:04
0:11:04
 0:01:13
0:01:13
 0:01:00
0:01:00
 0:12:55
0:12:55
 0:06:41
0:06:41
 0:01:26
0:01:26
 0:12:27
0:12:27
 0:03:34
0:03:34
 0:02:45
0:02:45
 0:16:58
0:16:58
 0:00:34
0:00:34