filmov
tv
A strange differential equation y''*(y-1)=y'

Показать описание
Solve y''*(y-1)=y', I misread the original problem from Maxime but I got this! Still cool!
A strange differential equation y''*(y-1)=y'
Solve the Initial Value Problem: y'(t) = t/y with y(1) = 2
everybody's first differential equation y'=y
Solve for y in: 2/y+1 + 1-y/y = 1/y^2 +y
Solve the differential equation (y^2 + xy^2)y’ = 1
Non-Linear Differential Equation: y'' + (y')^2 + 1 = 0
Solve the differential equation (y + sin y) y’ = x + x^3
Differential Equations | Solving y'=y five ways!
Applications of Euler's Identity, Trying out ACT Math Questions, Arrangements of 6 People in 3 ...
A Differential Equation with Euler's Number
Solving the Differential Equation y''=(y')^2
Can y'*y''=y'''? (WolframAlpha didn't find all the solutions)
5 simple unsolvable equations
How to Solve a Differential Equation with Series (x - 1)y'' - xy' + y = 0 with y(0) =...
Find a Differential Equation whose Solution is y = a*ln(bx)
Solve using the Method of Undetermined Coefficients (1/4)y'' + y' + y = x^2 - 3x
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Solve a differential equation by substitution, v=x^3+y^3, an exam question
A Differential Equation With An Interesting Solution
An Interesting Differential Equation, y=(y')^2
Find dy/dx if y= x cosy | Differential calculus
Creating a differential equation
Non Linear 2nd Order Differential Equation: y'' = yy'
(DE09) Basic Theory of Higher-Order ODE's
Комментарии
 0:09:27
0:09:27
 0:03:48
0:03:48
 0:07:31
0:07:31
 0:08:53
0:08:53
 0:02:53
0:02:53
 0:02:54
0:02:54
 0:02:04
0:02:04
 0:10:14
0:10:14
 3:28:09
3:28:09
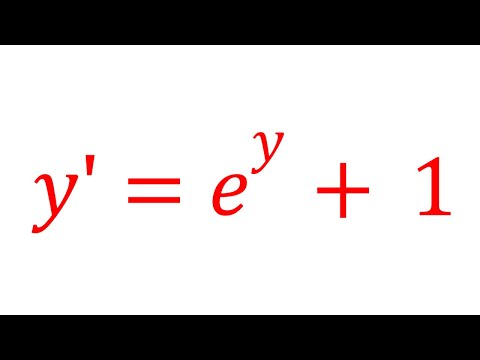 0:07:36
0:07:36
 0:09:19
0:09:19
 0:14:58
0:14:58
 0:00:50
0:00:50
 0:35:06
0:35:06
 0:03:21
0:03:21
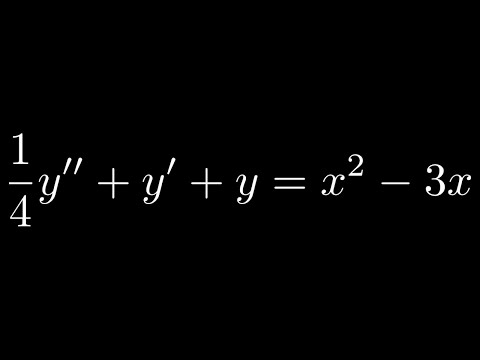 0:12:04
0:12:04
 0:00:15
0:00:15
 0:06:04
0:06:04
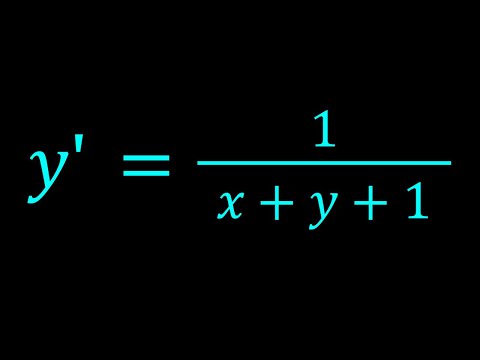 0:10:40
0:10:40
 0:09:40
0:09:40
 0:02:29
0:02:29
 0:00:23
0:00:23
 0:03:07
0:03:07
 0:37:00
0:37:00