filmov
tv
Theory of numbers: Quadratic residues

Показать описание
This lecture is part of an online undergraduate course on the theory of numbers.
We define quadratic residues (squares) and describe their basic properties, in particular Euler's criterion. The we describe fast algorithms to test whether a number is a quadratic residue, and if so to find its square root.
We define quadratic residues (squares) and describe their basic properties, in particular Euler's criterion. The we describe fast algorithms to test whether a number is a quadratic residue, and if so to find its square root.
Number Theory | Quadratic Residues: Definition and Examples
Theory of numbers: Quadratic residues
What is a Quadratic Residue? - Definition and Example
number theory 6- 5 Quadratic Residues
What is Quadratic Residue in Number Theory | Math Olympiad, ISI CMI Entrance
Quadratic Residues -- Number Theory 22
Legendre Symbol Definition and Example
A Nice Problem | What is Quadratic Residue? | Number Theory
Quadratic residue|quadratic residues number theory|quadratic residue modulo example|find quadratic
(Quadratic Residues) - The Multiplication Table for Quadratic Residues
Quadratic Residues — Number Theory 22
Quadratic Residues Always Have Even Index
Number Theory | How many quadratic residues mod p??
Quadratic Residues, Legendre's symbol and Proof of Euler's Criterion in Number Theory.
Number Theory | Quadratic Residues
Quadratic Residue (Part-2) Definition of Quadratic Residue
QUADRATIC residue
LSU Number Theory Lecture 22 quadratic residues
[Quadratic Residues] - What are Quadratic Residues?
(Quadratic Residues) - Euler's Criterion for the Legendre Symbol
Number Theory | The Legendre Symbol and Euler's Criterion
Quadratic residue and non quadratic residue in hindi 🔥
Quadratic Residues in Number Theory - With Examples | Cryptography and Coding Theory (With Notes) 🔥...
Number Theory | Quadratic Reciprocity Examples
Комментарии
 0:04:44
0:04:44
 0:29:07
0:29:07
 0:04:53
0:04:53
 0:04:13
0:04:13
 0:07:59
0:07:59
 0:32:01
0:32:01
 0:02:08
0:02:08
 0:10:52
0:10:52
 0:03:55
0:03:55
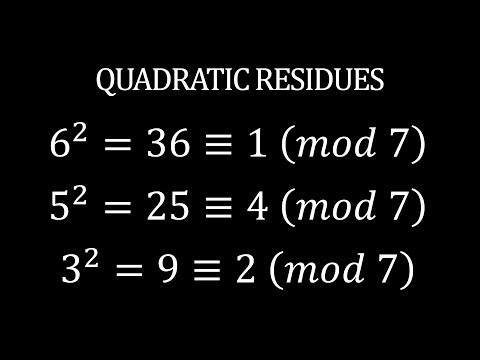 0:03:34
0:03:34
 0:32:01
0:32:01
 0:07:53
0:07:53
 0:06:45
0:06:45
 0:40:44
0:40:44
 0:04:45
0:04:45
 0:05:29
0:05:29
 0:05:12
0:05:12
 1:02:32
1:02:32
![[Quadratic Residues] -](https://i.ytimg.com/vi/EJv4TiYP8-s/hqdefault.jpg) 0:04:26
0:04:26
 0:05:40
0:05:40
 0:10:28
0:10:28
 0:03:13
0:03:13
 0:05:44
0:05:44
 0:08:13
0:08:13