filmov
tv
Derivatives Exponential and Logarithmic Functions MCV4U TEST

Показать описание
#IBSL_exponential_derivatives #derivatives_of_exponential_functions_and_logarithmic_functions #anilkumarmath #globalmathinstitute #mcv4u
Q1. Simplify the following. Express all answers in exact form.
a. ln(e^2x )-ln(e^x ) b. 10^(-3 log10 )
c. (x+y)^(log_2π/log_2(x+y) ) d. e^(-4 ln2+2 ln4 )
Q2. If log_2P=x,log_2Q=y,log_2R=z, write log_2((R^2 √Q)/P^3 ) in terms of x, y, and z.
Q3. Solve for x. Express in exact form.
a. log_2∛((x^2+30x) )=2 b. log_4〖x^3 〗+log_2√x=8
Q4. Sketch the graph of y=log_2(x+2)
Q5. Determine the derivative with respect to x. Simplify fully.
a. y=(1+5e^3x )^2 b. y=ln(e^x √x)
c. f(x)=e/lnx d. e^6x sin(5x^2 )
Q6. Determine the equation of tangent line, in standard form, to the graph of the function f(x)=sin(ln〖x^2 〗 ) at x = -1.
Q7. Determine whether the graph of y=xe^(4x+1) is concave up or concave down when x = -1.
Q8. Suppose f(x)= log_2(2x-1) find f^' (3).
Q9. Suppose f(x)=a ln(2x+b) where f(e)=3 and f^' (e)=6/e , find the constants a and b.
Q1. Simplify the following. Express all answers in exact form.
a. ln(e^2x )-ln(e^x ) b. 10^(-3 log10 )
c. (x+y)^(log_2π/log_2(x+y) ) d. e^(-4 ln2+2 ln4 )
Q2. If log_2P=x,log_2Q=y,log_2R=z, write log_2((R^2 √Q)/P^3 ) in terms of x, y, and z.
Q3. Solve for x. Express in exact form.
a. log_2∛((x^2+30x) )=2 b. log_4〖x^3 〗+log_2√x=8
Q4. Sketch the graph of y=log_2(x+2)
Q5. Determine the derivative with respect to x. Simplify fully.
a. y=(1+5e^3x )^2 b. y=ln(e^x √x)
c. f(x)=e/lnx d. e^6x sin(5x^2 )
Q6. Determine the equation of tangent line, in standard form, to the graph of the function f(x)=sin(ln〖x^2 〗 ) at x = -1.
Q7. Determine whether the graph of y=xe^(4x+1) is concave up or concave down when x = -1.
Q8. Suppose f(x)= log_2(2x-1) find f^' (3).
Q9. Suppose f(x)=a ln(2x+b) where f(e)=3 and f^' (e)=6/e , find the constants a and b.
Derivatives of Logarithmic and Exponential Functions
Derivative of Logarithmic Functions
Derivatives of Exponential Functions
Exponential functions differentiation intro | Advanced derivatives | AP Calculus AB | Khan Academy
Derivatives of Exponential and Logarithmic Functions (Tagalog/Filipino Math)
Calculus 2 Lecture 6.3: Derivatives and Integrals of Exponential Functions
Derivatives of Exponential and Logarithmic Functions (Live Stream)
Take the derivative of the natural log function
Differentiation Class 12 Math in Bengali | HS 2025 | Calculus | WBCHSE | Aditya Sir | Let’s Improve...
[CALCULUS] Derivatives of Exponential and Logarithmic Functions
DERIVATIVE OF AN EXPONENTIAL FUNCTION || BASIC CALCULUS
XII (12th) Maths, Derivative Rules for Logarithm & Exponential Functions | Chap 4
Derivatives of Exponential and Logarithmic Functions [Chapter 3 Lesson 7]
Derivatives of Exponential, Logarithmic and Trigonmetric functions
Derivatives: Exponential and Logarithmic Functions
DIFFERENTIATING LOGARITHMIC FUNCTIONS
Logarithmic Function Differentiation
Differentiating Logarithmic Functions
Derivatives of Exponential and Logarithmic Functions
Derivative of exponential and logarithmic function (calculas) | 3sec mathophobia
Derivatives of exponential & logarithmic Functions ll Differentiation ll the concept classes ll
Introduction to Logarithmic Differentiation
Derivatives of Exponential Functions | Formulas and Sample Problems | Basic Calculus
More Chain Rule (NancyPi)
Комментарии
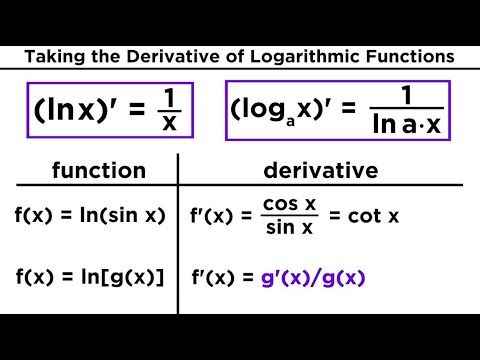 0:08:41
0:08:41
 0:12:13
0:12:13
 0:12:03
0:12:03
 0:05:24
0:05:24
 0:19:25
0:19:25
 1:30:52
1:30:52
 0:57:45
0:57:45
 0:00:43
0:00:43
 1:23:40
1:23:40
![[CALCULUS] Derivatives of](https://i.ytimg.com/vi/FdOMC_Nh48g/hqdefault.jpg) 0:09:32
0:09:32
 0:08:19
0:08:19
 0:06:21
0:06:21
 0:58:05
0:58:05
 0:10:52
0:10:52
 0:02:57
0:02:57
 0:11:16
0:11:16
 0:08:32
0:08:32
 0:05:00
0:05:00
 0:07:50
0:07:50
 0:21:02
0:21:02
 0:04:48
0:04:48
 0:13:31
0:13:31
 0:11:00
0:11:00
 0:11:56
0:11:56