filmov
tv
A Proof for the Twin Primes Conjecture

Показать описание
This video is an overview of my proof for the Twin Primes Conjecture, a long-standing open question in mathematics. I hope that it will give a decent understanding of my method and a measure of confidence in my result.
The paper I wrote to explain in more detail:
Come join the Discord as well!
The paper I wrote to explain in more detail:
Come join the Discord as well!
Twin Proofs for Twin Primes - Numberphile
Twin Prime Conjecture - Numberphile
The Fallacy of The Twin Primes Conjecture.
Goldbach Conjecture (but with TWIN PRIMES) - Numberphile
Einstein's twin paradox explained - Amber Stuver
A Simple Yet Absolute Proof of the Twin Primes Conjecture
I SOLVED THE TWIN PRIME CONJECTURE
Discrete Math - Proof: Sum of twin primes is divisible by 12 (Request)
twin prime conjecture proof
reciprocals of twin primes
dressing up with my twin :0
PROOF MY TWIN IS REAL
The indisputable proof that Fuwawa is, in fact, the evil twin
(Simplest) Proof of Twin Primes and Poliganc's Conjectures
Salish Matter and her twin 😳🥺 #nalish #shorts #twins #trending #trend #cute #shortsfeed #tiktok #fyp...
What is the Twin Paradox Example🤔 Neil deGrasse Tyson explained #science #physics #universe
5 Signs That Only Happen To Twin Flames 😮
Special Relativity Part 2: Time Dilation and the Twin Paradox
The Twins Paradox Hands-On Explanation | Special Relativity Ch. 8
😭Proof That TWIN Telepathy is REAL! 💀 #shorts #twins
Twin prime conjecture proof. Twin primes matrix system.
Shanks Has An Evil Twin: ALL EVIDENCE
Twin Prime Gap Explained [2014]
3 Signs to know it is Your Twin Flame #Shorts
Комментарии
 0:15:13
0:15:13
 0:17:42
0:17:42
 0:04:20
0:04:20
 0:11:49
0:11:49
 0:06:16
0:06:16
 0:07:26
0:07:26
 0:00:37
0:00:37
 0:04:35
0:04:35
 0:00:29
0:00:29
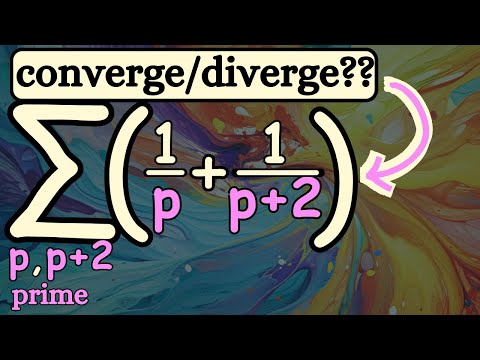 0:15:11
0:15:11
 0:00:15
0:00:15
 0:00:09
0:00:09
 0:02:25
0:02:25
 0:57:17
0:57:17
 0:00:13
0:00:13
 0:01:00
0:01:00
 0:00:40
0:00:40
 0:08:49
0:08:49
 0:04:05
0:04:05
 0:00:26
0:00:26
 0:15:40
0:15:40
 0:17:31
0:17:31
 0:02:35
0:02:35
 0:00:59
0:00:59