filmov
tv
Can You Simplify Another Radical?
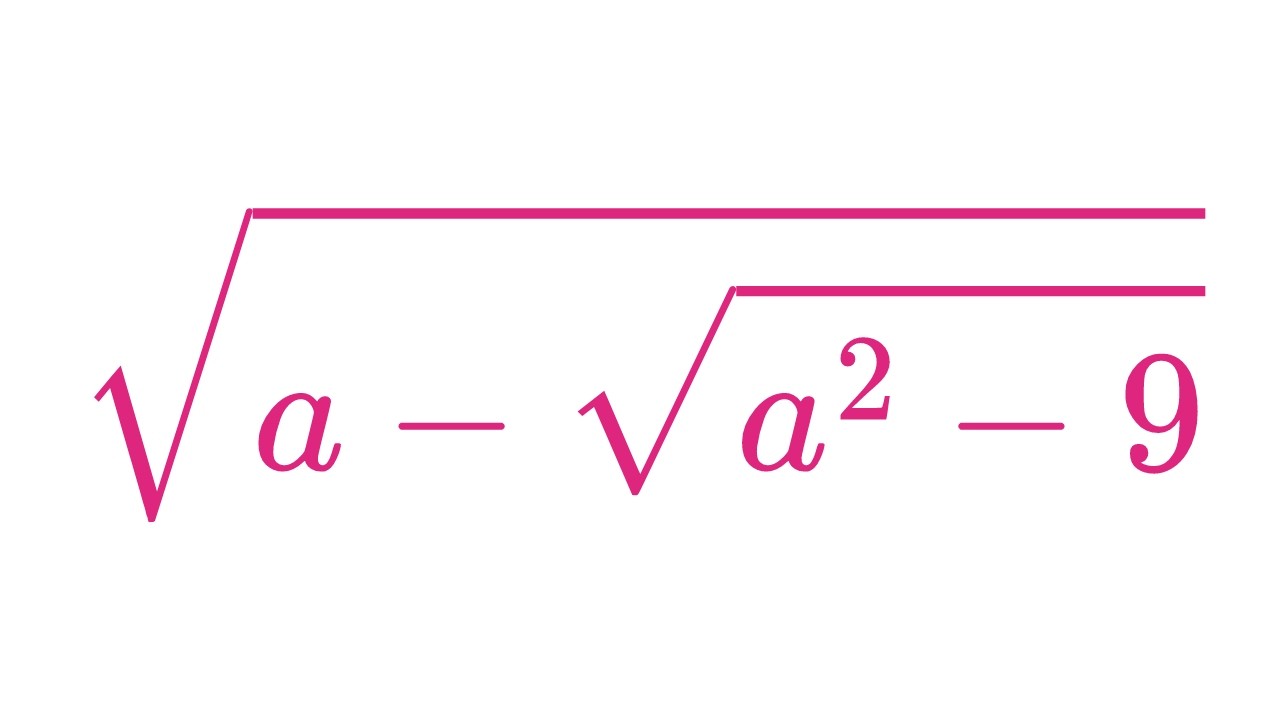
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Can You Simplify Another Radical?
Simplifying Radicals Easy Method
How to Simplify Radicals #1 #Shorts #math #maths #mathematics #education #learn #learning
CAN YOU SIMPLIFY #math #algebra #radical #youtubeshorts #shortvideo #shorts
CAN YOU SIMPLIFY #math #radical #youtubeshorts #shortvideo #shorts
Simplifying a Radical
Multiplying Radicals and Then Simplifying
Simplifying Radicals #2 #Shorts #algebra #math #maths #mathematics #education #learn #lesson #howto
CAN YOU SIMPLIFY #maths #algebra #radical #youtubeshorts #shortvideo #shorts
Math - Simplifying Radicals
How To Simplify Radicals
Simplifying A Nice Radical Expression
How to Multiply Radicals! 📚 #Shorts #algebra #math #maths #mathematics
Simplify A Radical Expression in 15 SECONDS or Less!
Simplifying A Very Radical Expression | Denesting Radicals
Simplify a radical expression with variables
Simplifying radicals multiplied by an integer
Simplifying Radicals #3 #Shorts #algebra #math #maths #mathematics
Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
Simplifying Radicals with Variables and Exponents
Simplify Radicals without Variables #math
Can you Simplify Radical problem ? #shorts
3 Problems to Challenge You Simplifying Radicals
Simplifying an Infinite Radical | My First Short
Комментарии
 0:10:41
0:10:41
 0:03:42
0:03:42
 0:00:11
0:00:11
 0:00:55
0:00:55
 0:00:59
0:00:59
 0:00:36
0:00:36
 0:04:05
0:04:05
 0:00:12
0:00:12
 0:00:51
0:00:51
 0:10:14
0:10:14
 0:13:14
0:13:14
 0:00:39
0:00:39
 0:00:22
0:00:22
 0:00:25
0:00:25
 0:08:43
0:08:43
 0:05:14
0:05:14
 0:01:58
0:01:58
 0:00:36
0:00:36
 0:11:20
0:11:20
 0:03:23
0:03:23
 0:00:58
0:00:58
 0:00:58
0:00:58
 0:07:19
0:07:19
 0:00:45
0:00:45