filmov
tv
3D Rocket Trajectories Introduction | Rocket Trajectories 5

Показать описание
Welcome to the introduction to rocket trajectories in 3 dimensions. In this rocket trajectories series, we’ve gone over the ideal rocket equation derivation, sounding rocket trajectories (1 dimensional motion), maximum dynamic pressure (or max Q), gravity turn rocket trajectories (2 dimensional motion), and now we are ready to take the next step into the 3rd dimension.
Modeling rocket trajectories in 3D will require knowledge on a number of different calculus, linear algebra and geometry topics, which include:
Ordinary differential equations, ODE solvers, 3D vectors which can represent position, velocity, 2D planes, and axes of rotation, active vs. passive rotations, rotation matrices, inertial and non-inertial reference frames, latitudinal to rectangular coordinates systems conversions, cross products for calculating axes of rotation and for calculating linear velocity from angular velocity, and more.
So once we have a solid understanding of these topics, we can begin to create very exciting simulations of rocket trajectories targeting specific orbital elements (like orbital inclination, eccentricity, and right ascension ) from different launch sites around the world.
Like in this simulation, where these are two stage rocket trajectories to orbit from Cape Canaveral, Vandenberg Air Force Base, French Guiana, Baikonur Cosmodrome, and Satish Dhawan.
Next up in this series is the relationship between launch azimuth, orbital inclination ,and launch site latitude, where we will be going over how to calculate the pitchover maneuver thrust acceleration vector to align the rocket to the proper launch azimuth to achieve the target orbital inclination and why the minimum inclination a rocket can achieve is equivalent to the latitude coordinate that they are launching from.
#rockettrajectories #rockettrajectorysimulations #rockettrajectory
Modeling rocket trajectories in 3D will require knowledge on a number of different calculus, linear algebra and geometry topics, which include:
Ordinary differential equations, ODE solvers, 3D vectors which can represent position, velocity, 2D planes, and axes of rotation, active vs. passive rotations, rotation matrices, inertial and non-inertial reference frames, latitudinal to rectangular coordinates systems conversions, cross products for calculating axes of rotation and for calculating linear velocity from angular velocity, and more.
So once we have a solid understanding of these topics, we can begin to create very exciting simulations of rocket trajectories targeting specific orbital elements (like orbital inclination, eccentricity, and right ascension ) from different launch sites around the world.
Like in this simulation, where these are two stage rocket trajectories to orbit from Cape Canaveral, Vandenberg Air Force Base, French Guiana, Baikonur Cosmodrome, and Satish Dhawan.
Next up in this series is the relationship between launch azimuth, orbital inclination ,and launch site latitude, where we will be going over how to calculate the pitchover maneuver thrust acceleration vector to align the rocket to the proper launch azimuth to achieve the target orbital inclination and why the minimum inclination a rocket can achieve is equivalent to the latitude coordinate that they are launching from.
#rockettrajectories #rockettrajectorysimulations #rockettrajectory
Комментарии
 0:03:33
0:03:33
 0:07:38
0:07:38
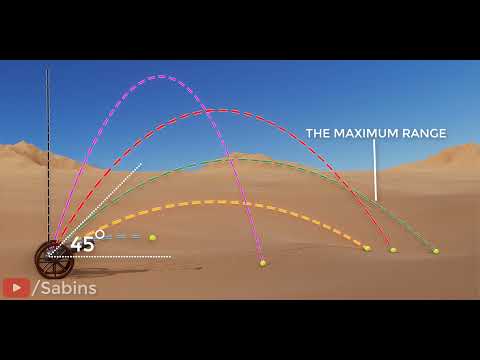 0:05:09
0:05:09
 0:00:46
0:00:46
 0:00:55
0:00:55
 0:00:59
0:00:59
 0:16:36
0:16:36
 0:00:31
0:00:31
 0:00:39
0:00:39
 0:00:25
0:00:25
 0:06:06
0:06:06
 0:14:20
0:14:20
 0:08:58
0:08:58
 0:06:46
0:06:46
 0:02:44
0:02:44
 0:00:17
0:00:17
 0:00:39
0:00:39
 0:07:06
0:07:06
 0:07:49
0:07:49
 0:01:39
0:01:39
 0:00:08
0:00:08
 0:05:59
0:05:59
 0:51:12
0:51:12
 0:00:31
0:00:31