filmov
tv
Calculer la limite d'une suite géométrique (3) - Terminale

Показать описание
Dans cette vidéo tu pourras apprendre à calculer la limite d'une suite géométrique. 👍
Calculer la limite d'une suite à l'aide des formules d'opération - Terminale
Déterminer la limite d'une suite - Première
1 minute pour la limite d'une suite
Calcul de la limite d'une suite numérique avec des puissances. TERMINALE
Limites de suites - Terminale
Calculer la limite d'une suite géométrique (1) - Terminale
Calculer la limite d'une suite avec une forme indéterminée (1) - Terminale
Calculer la limite d'une suite avec une forme indéterminée (2) - Terminale
Prépa- Développements limités - un beau classique
Calcul de la limite d'une suite numérique
Calculer la limite d'une suite avec une forme indéterminée (4) - Terminale
Calculer la limite d'une suite à l'aide du théorème de comparaison - Terminale
Terminale S méthode 4 : Trouver la LIMITE d'une SUITE CONVERGENTE- suite croissante majorée : c...
Calculer la limite d'une suite géométrique (3) - Terminale
Tale - Méthodes: Déterminer la limite d'une suite
Comprendre la notion de LIMITE d'une SUITE - Première
Calculer la limite d'une somme de termes d'une suite géométrique - Terminale
Limites de suite avec cos(n)
suites numériques || Calculer la limite d'une suite 3
Calculer la limite d'une suite géométrique (2) - Terminale
COMMENT CALCULER LA LIMITE D'UNE SUITE GÉOMÉTRIQUE
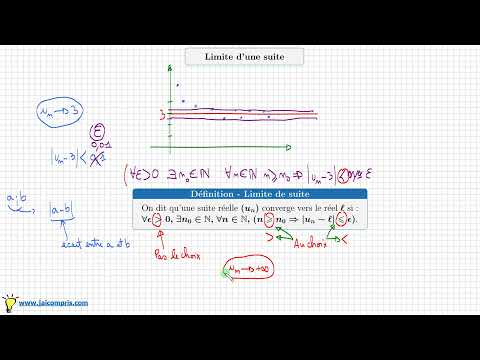
Limite d'une suite • Comprendre la définition avec epsilon et les quantificateurs • ∀ ∃ prépa M...
Calculer la limite d'une suite avec une forme indéterminée (3) - Terminale
Comment calculer la limite d'une suite du type q^n ?
Комментарии
 0:10:16
0:10:16
 0:06:16
0:06:16
 0:01:14
0:01:14
 0:03:09
0:03:09
 0:13:56
0:13:56
 0:08:27
0:08:27
 0:07:38
0:07:38
 0:08:23
0:08:23
 0:05:50
0:05:50
 0:03:46
0:03:46
 0:06:19
0:06:19
 0:05:01
0:05:01
 0:09:38
0:09:38
 0:06:17
0:06:17
 0:12:29
0:12:29
 0:10:37
0:10:37
 0:00:55
0:00:55
 0:00:29
0:00:29
 0:07:08
0:07:08
 0:03:57
0:03:57
 0:07:26
0:07:26
 0:08:55
0:08:55
 0:01:59
0:01:59