filmov
tv
Differentiation of Logarithmic, Exponential, Parametric & Successive Differentiation | Calculus
Показать описание
Welcome to Engineering Essentials! In this video, we dive deep into the Differentiation of Logarithmic, Exponential, and Parametric Functions along with Successive Differentiation. This detailed explanation is a part of our Calculus playlist, aimed at simplifying key concepts for engineering students. We cover: - How to differentiate logarithmic functions. - The rules for differentiating exponential functions. - Step-by-step differentiation of parametric equations. - An introduction to successive differentiation, where derivatives are taken multiple times. This video is perfect for bachelor's degree engineering students from top universities like IITs, NITs, MIT, and other leading institutions worldwide. Master these fundamental calculus techniques to excel in your coursework and exams.
#calculus #class11 #class11maths #maths #englishmedium #cbse #differentiation
🔑 Keywords: Differentiation, Logarithmic Functions, Exponential Functions, Parametric Differentiation, Successive Differentiation, Calculus, Engineering Mathematics, IIT JEE, MIT, NITs, Ivy League Colleges
📌 Hashtags: #Calculus #Differentiation #LogarithmicFunctions #ExponentialFunctions #ParametricEquations #SuccessiveDifferentiation #EngineeringEssentials #IITJEE #MIT #EngineeringStudents
Differentiation of Logarithmic, Exponential, Parametric Form | Successive Differentiation #maths #eranand
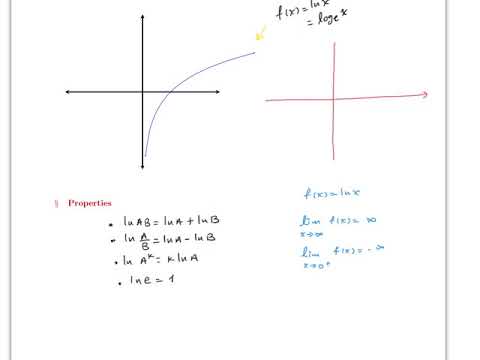
In mathematics, a differentiable function is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A function is said to be continuously differentiable if its derivative is also a continuous function; there exist functions that are differentiable but not continuously differentiable
Differentiation is a fundamental concept in calculus that is used to find the rate of change of a function. The derivative of a function is a new function that gives the slope of the tangent line to the original function at a given point.
Differentiation can be used to solve a wide variety of problems. For example, it can be used to find the maximum and minimum values of a function, to determine the rate of growth or decay of a quantity, and to find the slope of a tangent line.
Differentiation is a powerful tool that can be used to analyze functions and solve problems. It is an essential concept in calculus and is used in many different fields, including physics, chemistry, engineering, and economics.
Here are some additional examples of how differentiation is used:
In physics, differentiation can be used to find the acceleration of a moving object.
In chemistry, differentiation can be used to find the rate of reaction of a chemical reaction.
In engineering, differentiation can be used to find the stresses and strains on a structure.
In economics, differentiation can be used to find the rate of change of a company's profits.
Differentiation is a versatile tool that can be used to solve problems in many different fields. It is an essential concept in calculus and is used by scientists, engineers, and economists to analyze data and solve problems.
#calculus #class11 #class11maths #maths #englishmedium #cbse #differentiation
🔑 Keywords: Differentiation, Logarithmic Functions, Exponential Functions, Parametric Differentiation, Successive Differentiation, Calculus, Engineering Mathematics, IIT JEE, MIT, NITs, Ivy League Colleges
📌 Hashtags: #Calculus #Differentiation #LogarithmicFunctions #ExponentialFunctions #ParametricEquations #SuccessiveDifferentiation #EngineeringEssentials #IITJEE #MIT #EngineeringStudents
Differentiation of Logarithmic, Exponential, Parametric Form | Successive Differentiation #maths #eranand
In mathematics, a differentiable function is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain. A function is said to be continuously differentiable if its derivative is also a continuous function; there exist functions that are differentiable but not continuously differentiable
Differentiation is a fundamental concept in calculus that is used to find the rate of change of a function. The derivative of a function is a new function that gives the slope of the tangent line to the original function at a given point.
Differentiation can be used to solve a wide variety of problems. For example, it can be used to find the maximum and minimum values of a function, to determine the rate of growth or decay of a quantity, and to find the slope of a tangent line.
Differentiation is a powerful tool that can be used to analyze functions and solve problems. It is an essential concept in calculus and is used in many different fields, including physics, chemistry, engineering, and economics.
Here are some additional examples of how differentiation is used:
In physics, differentiation can be used to find the acceleration of a moving object.
In chemistry, differentiation can be used to find the rate of reaction of a chemical reaction.
In engineering, differentiation can be used to find the stresses and strains on a structure.
In economics, differentiation can be used to find the rate of change of a company's profits.
Differentiation is a versatile tool that can be used to solve problems in many different fields. It is an essential concept in calculus and is used by scientists, engineers, and economists to analyze data and solve problems.
0:04:16
0:12:13
0:12:03
0:10:48
0:13:31
0:06:33
0:00:43
1:30:52
0:05:11
0:23:29
0:13:07
0:14:02
0:09:40
0:22:37
0:05:57
0:11:53
0:16:49
0:07:50
0:02:34
0:04:21
0:04:15
0:00:32
0:10:14
0:17:26