Can You Figure It Out? The *Almost* Impossible Geometry Puzzle Solved. [Not Clickbait]

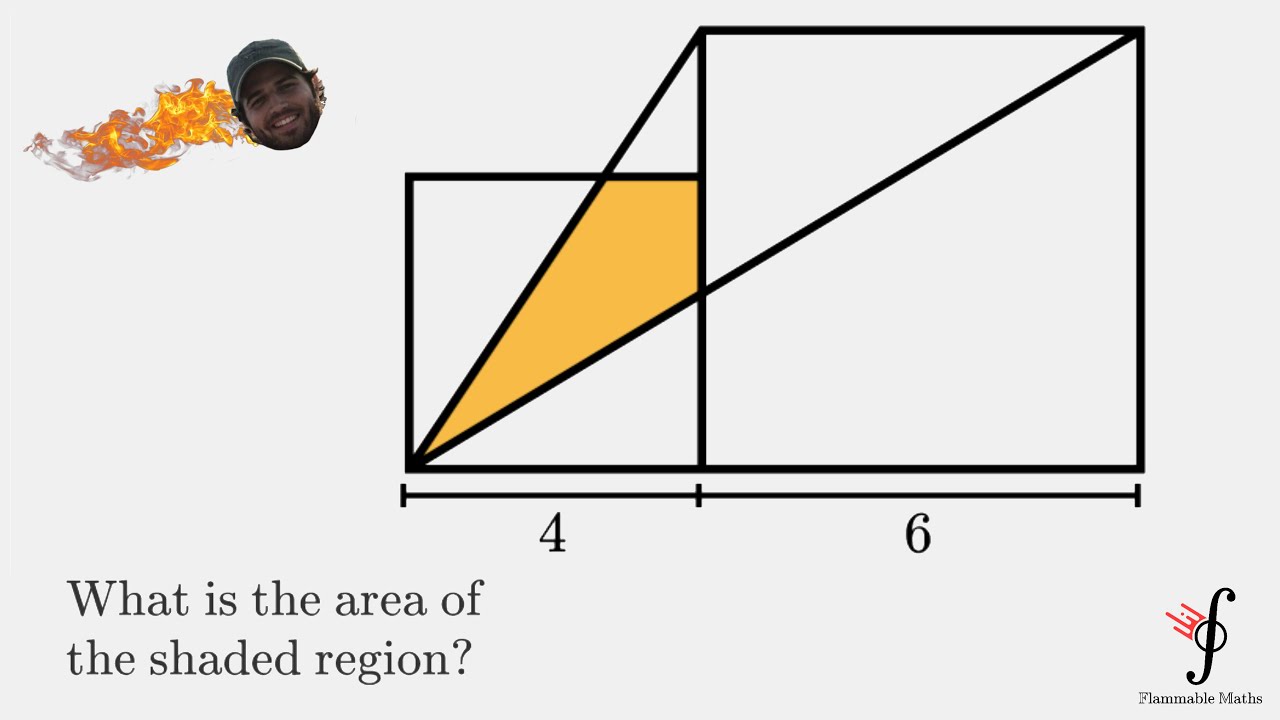
Today we want to find the shaded area :v We use analytic geometry to get the job done :3 Enjoy! =D

Help me create more free content! =)

--------------------------------------------------------------------------------
Wanna send me some stuff? lel:

Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------

#FreshT #DidYouFigureItOut?

[wjx]

you can also use similar triangles to solve the problem.
first break the shaded region into two triangles by drawing the diagonal of the square.
and now use similar triangles to find the length of the two tips.
(4-x)/x=4/(6-4) which leads to x=4/3.
(y+2)/(4-y)=6/4 which leads to y=8/5.
hence the area of the shaded region is x*4/2+y*4/2=2(4/3+ 8/5)=88/15.

[michaelz]

Why do I have a sudden urge to go "Mind your decisions, I'm Presh Talwalker"? By the way, I hear this problem was only solved by percent of high school seniors in Croatia.

[aarryasaraf]

I want mama flammy to react to the why analytic is the best part

[hkefdsu]

Where is the book advertisement? The loud ting ting ting ting, the clickbait?

[mintsjams]

There's nothing better than an overly complicated but absolutely elegant answer to a math problem

[OlliWilkman]

Another way with similar triangles: the whole 4-square is broken into two right-angle triangles plus the shaded region. Then the shaded area is 16 minus the two triangles.

From similar triangles we get that the upper triangle has a short side 8/3 and the lower has short side 12/5. The area of a triangle is width*height/2, so the upper triangle has area 16/3 and the lower is 24/5. So the final answer is 16 – 24/5 – 16/3, which is 240/15 – 80/15 – 72/15 = 88/15.

[BiscuitZombies]

I simply turned the two diagonals into linear equations with y intercept at 0. y = mx = rise/run.
- So you get y1 = 3x/5, y2 = 3x/2. Integrate y2-y1 from 0 to 4 = 36/5. That is the triangle area (the shaded region + the small triangle on top). {You could alternatively use similar triangles to find the area of the smaller triangle on the bottom then subtract that from the right triangle = 4*6/2 - A(small triangle on bottom).}
- Then the horizontal line which is the base of the smaller triangle is simply y = 4.
- So find the intersection point of y2 and 4 == x=8/3. So integrate from 8/3 to 4 on y2-4 to get the small triangle area = 4/3.
- Now do the triangle - smaller triangle = 36/5-4/3 = 88/15.
Done. This way you don't have y intercepts.

[shaiavraham]

I have no problem with killing this problem with analytic geometry (I'll take analytic geometry over geometry every day), but did you really need to use an integral to calculate the area of trapezoid?

[ms.psfunclassroom]

I solved this problem by comparing triangles' ratio.

[notabotta]

Papa, please keep up the clickbait-style videos occasionally. While the math may not be that rigorous, I enjoy being able to actually solve all of these problems by hand and give myself harder or generalized versions to try. I learn a lot from your other videos, but this gives me the chance to practice what I already know. Just a suggestion!

[heisenberg]

*Me seeing the Problem*
Me: "Integarahl"

[LightPhoenix]

I did it mostly similarly, but left the squares unrotated with the origin on the left corner. Calculated the formulas for the lines, and calculated the points on the squares, and the area as the area of the small square minus the areas of the two triangles.

[kingdomadventures]

This is great for brilliant.com because their brilliant solutions have always been common knowledge but for a price.

[MrRyanroberson]

11:00 bruh me too. analytic geometry is totally reliable and much easier to write down, so it just naturally becomes easier to work with.

[raghualluri]

Amazing I really like these contest type problems!

[frandygil]

Papa, you commented on a video from what the hectogon? and said that you would do a video about the generalization of the integral of the powers of sine from 0 to pi/2, I want to know if you are still planning on doing it or if you did and i havent found it yet.

Also sorry for my english, I am from a Spanish speaking country.

[donkosaurus]

from the thumbnail






big triange = 6*6/2, take away RH triangle 36/10*6/2, take away upper triangle 4/3*2/2 finally gives 88/15

[xaytana]

Unless the problem asks for you to solve it in this specific way, would it not have been easier to just use scale to find the area of the triangles and subtract that from the square? All of this fits within a 6*6 rectangle, where one triangle is easily found, and the other is found by mirroring it by it's hypotenuse.

The square has an area of 16.
Triangle Aα, the larger variant of the smaller triangle. Side lengths of 4 and 6, area of 12. Scale factor of 2/3, side length 6 -> side length 4. Scale factor of area is scale factor squared, 12*(4/9)=16/3, which is the area of triangle Aβ, the smaller variant of the smaller triangle.
Triangle Bα, the larger variant of the larger triangle. Side lengths of 6 and 10, area of 30. Scale factor of 2/5, side length 10 -> side length 4. Scale factor of area is scale factor squared, 60*(4/25)=24/5, wich is the area of triangle Bβ, the smaller variant of the larger triangle.
This gives us triangle Aβ as 16/3, or 80/15, triangle Bβ as 24/5, or 72/15, and the square as 16, or 240/15.
Which gives us the equation of (240/15)-(80/15)-(72/15) -> (240-80-72)/15 -> 88/15, or 5.86̅

I know the content of your channel is more in line with how you solved this, but should we not also look at the most efficient way of solving problems? I get that higher level maths have their uses, and simpler problems like this could be good practice if you want what's possibly the simplest problem for this, but I think there's better applications of higher level maths when a problem as simple as this one can be solved with scale, a concept taught in the most basic of geometry lessons; I believe I was taught scale in elementary school here in the States when I was a kid, although the scaled area being a square of scale factor wasn't taught until later, but you can still do this problem with scale alone, it's just not as efficient. On Brilliant's sword rating, I wouldn't even consider this a 1, as it's something a literal primary school child could do, considering all you need is arithmetic and one of the earliest concepts taught in geometry.
It's like trying to measure a long distance with a single stick, rather than a much longer tape measure, you're just needlessly creating more work for yourself.

[zivssps]

You can solve that question under 2 minutes by doing the following steps:
1. Mark all the points on the XY plane, starting with the left bottom point as (0, 0) and so on.
2. Calculate the lines' equations of the lines around the shaded area [y=1.5x, y=0.6x, y=4, x=4].
3. Calculate the intersections points of thoes lines (the points of the shaded area) [(0, 0), (4, 2.4), (4, 4), (2.67, 4)].
4. Use the Gauss's Shoelace formula to find the area.
Wikipedia page about the Gauss's Shoelace formula:
An amazing
Mathologer video about the Gauss's Shoelace formula:

[angusheath]

Like for chad coordinate system and integration
Comment for simp similar triangles