Write the polynomial given conjugate irrational zeros

👉 Learn how to write the equation of a polynomial when given irrational zeros. Recall that a polynomial is an expression of the form ax^n + bx^(n-1) + . . . + k, where a, b, and k are constants and the exponents are positive integers. The zeros of a polynomial are the values of x for which the value of the polynomial is zero. Also recall that when the square root of a number (irrational zero) is a zero to a polynomial, the conjugate of the irrational zero will also be a zero to the polynomial.

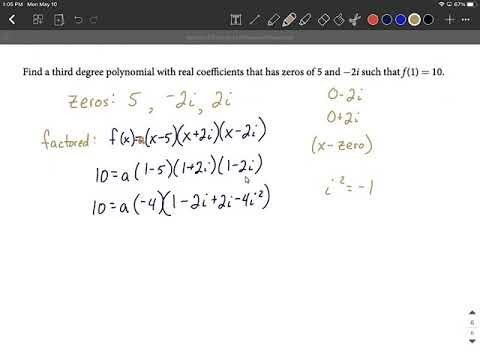
To write the equation of a polynomial, we write the given zeros in factor form and expand the product of the factors. Thus, given a, b, . . . as zeros to a polynomial, we write the equation of the polynomial by expanding the factors (x - a)(x - b) . . . = 0

Organized Videos:
✅Write the Equation of a Polynomial Given the Zeros
✅Write the Equation of a Polynomial Given Complex Zeros
✅Write the Equation of a Polynomial Given Zeros with Fractions
✅Write the Equation of a Polynomial Given Real Zeros
✅Write the Equation of a Polynomial Given Irrational Zeros
✅Write the Equation of a Polynomial Given Imaginary Zeros
✅Write the Equation of a Polynomial Given Zeros | Learn About

Connect with me:

#polynomials #brianmclogan

[liamtam]

how do you do the same thing if you are given zeros with imaginary numbers included? say {-3i, 2+3i} for example