Proof: Group Elements Have Unique Inverses | Abstract Algebra

preview_player
Показать описание
Groups contain elements, and each element has a unique inverse. This is not a group axiom, but it is true of all groups! We will be proving this basic group theory result in today's video lesson!

We'll need to remember that in a group, every element does have an inverse. For an element a, the inverse of a is the element b such that ab = ba = e, where e is the identity of the group. We'll also need to remember that group elements are associative under the group operation. With these two facts in mind, we'll easily be able to prove that each group element must have a unique inverse! For example, in the group of the integers under addition, the element 3 has the unique inverse of -3, and 7 has the unique inverse of -7.

I hope you find this video helpful, and be sure to ask any questions down in the comments!

********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.

********************************************************************
+WRATH OF MATH+

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Proof: Group Elements 0:04:29

Proof: Group Elements Have Unique Inverses | Abstract Algebra

Proof: Identity Element 0:02:42

Proof: Identity Element of a Group is Unique | Abstract Algebra

Proof that the 0:01:49

Proof that the identity element of a group is unique

Proof: Finite Order 0:07:58

Proof: Finite Order Elements Have n Distinct Powers | Abstract Algebra

Prove that every 0:02:37

Prove that every group element has a unique inverse (ILIEKMATHPHYSICS)

A Simple Group 0:05:25

A Simple Group Element Inverse Proof | Abstract Algebra

Identity Element: Examples 0:05:57

Identity Element: Examples and Uniqueness Proof

Proof: Group Element 0:03:15

Proof: Group Element is the Inverse of its Inverse | Abstract Algebra

Proof that the 0:03:30

Proof that the Identity Element in a Group is Unique

Proof: Elements that 0:03:03

Proof: Elements that Commute Have Commutative Inverses | Abstract Algebra

A Proof for 0:07:10

A Proof for the Uniqueness of the Identity Element in Group Theory

Identity element in 0:04:31

Identity element in a group is Unique | Theorem proof

How to Prove 0:03:16

How to Prove that an Identity Element of a Set G under a Binary Operation must be Unique, #FP2

Group Theory Basics: 0:00:40

Group Theory Basics: Unique Identity and Inverse Element Proof | Klassic #BSc3rdSemester

How to prove 0:04:26

How to prove identity elements are unique

Every group has 0:03:43

Every group has only one identity element (Proof) [ILIEKMATHPHYSICS]

Prove that identity 0:02:57

Prove that identity element in a group is unique !! ( Bsc semester 1 maths Hon's)

Theorem to prove 0:10:56

Theorem to prove inverse of any element in group G is Unique

A proof that 0:02:54

A proof that if an element (a) in a group has order n and if a^k = e then n|k

Inverse of each 0:07:51

Inverse of each element in a group is unique | theorem proof

Group Theory| Idempotent 0:05:08

Group Theory| Idempotent element | definition and theorem (proof)| Lec 6

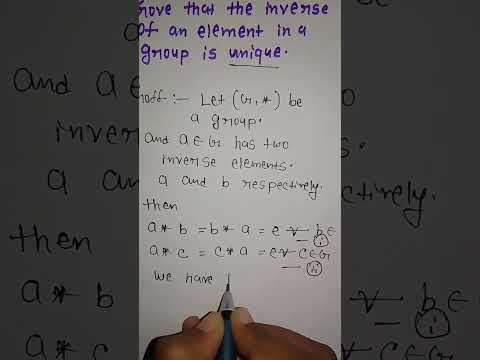Prove that the 0:04:57

Prove that the inverse element in a group is unique. ( Bsc semester 1 maths Hon's )

The identity element 0:06:43

The identity element is unique theorem (proof)

If a and 0:01:38

If a and b are distinct group elements, prove that either a^2 not equals b^2 or a^3 not equals b^3